大家好，我是想念你们的小兮兮♥(ˆ◡ˆԅ)~
好久没写数学文了，今日突然想起高考前我后桌同学问个一个题，便和大家继续聊聊圆锥曲线的光学性质。
圆锥曲线的光学性质其实本身是很有意思的，可是在日常的课堂上很少有老师认真的去讲这个点，往往是一笔带过，也导致出现了对应的应用学生也往往束手无策。
从这篇文章起，我的写文风格将会有所改观，日后敬请期待~
我们先看看教科书上对于圆锥曲线光学性质的讲解：
生活中的应用我先不说，但从数学上聊聊，它也有很多可以挖掘的地方。
一、椭圆
从椭圆的一个焦点射出光线，光线碰到椭圆边界反射后的路径经过另一个焦点。
即：椭圆两焦点分别与椭圆上任意一点连线，两条直线与过该点的切线夹角相等。
那么从这个定义，我们就能找出两组等角。
之后。。。
应该还有人记得我这篇文章吧~
我们令切线交 xx 轴于点 II ，同时做出切线的垂线，交 xx 轴于点 JJ .
那么可以得到 （）（I,J;B,C）（I,J;B,C） 为一组调和点列。
之后也可以从此出一系列的高考 （）（×）（×） 模拟题。
用角平分线定理，有： CACJ=BABJ=2a2c=1e\frac{CA}{CJ}=\frac{BA}{BJ}=\frac{2a}{2c}=\frac{1}{e}
张角定理我就不打了，会更好看。
这就是之前数圈创新卷我出的圆锥曲线的之一题。
其实第二问如果把光路图做出来也勉强和光学性质有点关系：两直线与圆锥曲线的四个交点四点共圆的充要条件是两直线倾斜角互补。
如果从点 II 再作直线与上面另外的三条直线交于三个点，同时也能保持交比不变，那么更多的圆锥曲线题产生了......
我们再想想椭圆的第三定义：
直线 、AC、ABAC、AB 斜率积为 e2−1e^2-1 ，又是无穷的小题。
二、双曲线
从双曲线的一个焦点射出光线，光线碰到双曲线边界反射后的路径的反向延长线经过另一个焦点。
即：双曲线两焦点分别与双曲线上任意一点连线，两条直线与过该点的切线夹角相等。
仿照上面对椭圆的讨论：
我们令切线交 xx 轴于点 FF ，同时做出切线的垂线，交 xx 轴于点 EE .
那么可以得到 （）（F,E;A,B）（F,E;A,B） 为一组调和点列。
用角平分线定理，有： ACAE=BCBE\frac{AC}{AE}=\frac{BC}{BE}
张角定理我也不打了，不过之前好像也出过这类的题。
我们再想想椭圆的第三定义：
直线 、AC、BCAC、BC 斜率积为 e2−1e^2-1 ，又是无穷的小题。
三、抛物线
从抛物线的焦点射出光线，光线碰到抛物线边界反射后的路径平行于抛物线的对称轴。
即：抛物线的焦点与抛物线上任意一点的连线和抛物线的对称轴与该点的切线的夹角相等。
这里有趣的是:
我们令切线交 xx 轴于点 GG ，同时做出切线的垂线，交 xx 轴于点 HH .
因为直线 EI//HGEI//HG ,则 EIEI 与 GHGH 交于无穷远点 P∞P_{\infty} .
那么可以得到 （）（G,H;C,P∞）（G,H;C,P_{\infty}） 为一组调和点列,则 CC 为 GHGH 中点。
其实这里面还有很多有趣的东西，补张图，有兴趣的同学可以自己探究。
书上给了这么一个综合题，我不想写了，但确实是一个很好的运用，解答留给读者。
下面我们来看看一些用到了上面光学性质的题目：
Q1:求对于切线方程
A1:极点极线。
①椭圆 b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) , P(x0,y0)P(x_{0},y_{0}) 为椭圆上一点，过 PP 作椭圆的切线 ll ，则 ll 的方程为 x0xa2+y0yb2=1\frac{x_{0}x}{a^2}+\frac{y_{0}y}{b^2}=1 .
②双曲线 0，b>0)">，x2a2−y2b2=1(a>0，b>0)\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0，b>0) , P(x0,y0)P(x_{0},y_{0}) 为双曲线上一点，过 PP 作双曲线的切线 ll ，则 ll 的方程为 x0xa2−y0yb2=1\frac{x_{0}x}{a^2}-\frac{y_{0}y}{b^2}=1 .
③抛物线 0)">y2=2px(x>0)y^2=2px(x>0) , P(x0,y0)P(x_{0},y_{0}) 为抛物线上一点，过 PP 作抛物线的切线 ll ，则 ll 的方程为 y0y=2p(x0+x2)y_{0}y=2p\left( \frac{x_{0}+x}{2} \right) .
Q2..给定椭圆b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)及其上一动点PP， ll 为过 PP 的切线， F′F 为椭圆其中一个焦点 FF 在 ll 上的投影，求 F′F 的对应轨迹.（该题与解答均来自
）A2: F′F 的运动轨迹为 x2+y2=a2x^2+y^2=a^2 。如图。
证明：
首先作 FF 关于 ll 的对称点 F1F_{1} ，连接 、、F1F0、PF、OF′F_{1}F_{0}、PF、OF ，如图。
由椭圆的光学性质可知， PP 在 F1F0F_{1}F_{0} 上。
又易知 OF′OF 为 △F0F1F\triangle F_{0}F_{1}F 的中位线，所以有 OF′=12F0F1=12(PF0+PF)=aOF=\frac{1}{2}F_{0}F_{1}=\frac{1}{2}(PF_{0}+PF)=a
即 F′F 到坐标原点 OO 的距离为定值 aa ，所以 F′F 的轨迹方程为 x2+y2=a2x^2+y^2=a^2.
Q3：
A3:
Q4：
A4:
Q5：
A5:
Q6:这个就是我同学问的，我觉得是一个很好的题。
已知抛物线 x^2=4y ，焦点为 F ,抛物线右侧上有一点 A ,若直线 AF 与过 A 点的切线的夹角为 30^\circ ,求 A 点纵坐标以及直线 AF 的斜率.
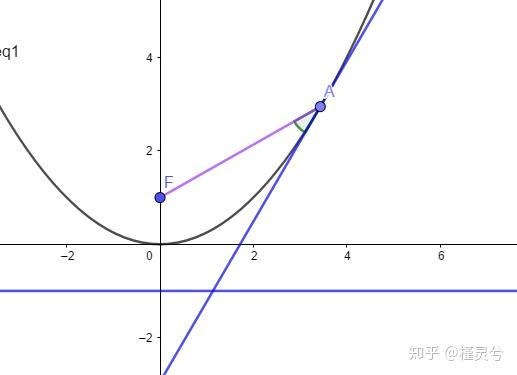
A6:
法一：当时我看到这道题，我也懒得想，我说了一句剥蒜（爆算）即可，他告诉我就是因为他觉得异常难算，于是才来问我，便有了下面的法二；
法二：
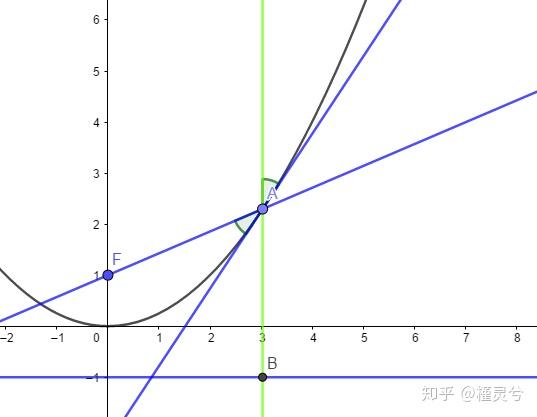
我们作出过 A 且平行于抛物线对称轴的直线（上面刻意用绿色标注）
依据抛物线的光学性质，直线 AF 的倾斜角应该是直线 AF 与过 A 点的切线的夹角的余角， k_{AF}=tan(90^\circ-30^\circ)=tan60^\circ=\sqrt{3} .
由圆锥曲线统一极坐标公式：\rho=\frac{ep}{1-ecos\theta} ，则 AB=AF=\frac{2}{1-cos60^\circ}=4=y_A+\frac{p}{2} .
则 y_A=3 .
圆锥曲线的光学性质也差不多就到这里了，上面也选取了一些经典例题，希望大家能有所收获。
之后不定时更文，望多多包涵。
祝君好运~
