『解析几何』光学性质之美

2020年2月26日更新。

在b站传了配套的解说，同学们有需自取。

前言(Introduction)

23号刚考完了期末考，在生物考试上想到了关于圆锥曲线的光学性质，觉得很美。就想要写一篇文来介绍一下三种圆锥曲线的光学性质。然后因为证明过程中要用到一些定理，所以感觉这篇文可能会有点长…？

阅读须知(Instructions)

1.编辑不易，收藏同时不要忘记点赞。有兴趣继续跟进的话还可以关注我。

2.本文中所介绍的光学性质并不能够在考试中直接用，并且用起来要证明的话所占空间也较多。所以主要作为一种性质来欣赏以及研究相关衍生的结论。

3.阅读全文大约需要25分钟。请耐心食用。

正文(Main body)

1.配积定理

或者又可称为极线方程。（其实“配积定理”这个名字很有可能是我老师独创的…不过也将就用着吧）（补充：根据评论区反馈，或许叫做“配极定理”…？）

定理：

①给定椭圆 b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) , P(x0,y0)P(x_{0},y_{0}) 为椭圆上一点，过 PP 作椭圆的切线 ll ，则 ll 的方程为 x0xa2+y0yb2=1\frac{x_{0}x}{a^2}+\frac{y_{0}y}{b^2}=1 。

②给定双曲线 x2a2−y2b2=1\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 , P(x0,y0)P(x_{0},y_{0}) 为双曲线上一点，过 PP 作双曲线的切线 ll ，则 ll 的方程为 x0xa2−y0yb2=1\frac{x_{0}x}{a^2}-\frac{y_{0}y}{b^2}=1 。

③给定抛物线 0)">y2=2px(x>0)y^2=2px(x>0) , P(x0,y0)P(x_{0},y_{0}) 为抛物线上一点，过 PP 作抛物线的切线 ll ，则 ll 的方程为 y0y=px0+pxy_{0}y=px_{0}+px 。

到这里，大家应该都看出了这其中的规律了吧。保留常数项不变，含有变量的项进行对应变化： 、x×x⇒x0×x、px+px⇒px0+pxx\times x\Rightarrow x_{0}\times x、px+px\Rightarrow px_{0}+px 。凡是二次的就降成一次，凡是一次的就分成两半。其实对于任意的不规则的二次曲线这个定理都成立，不过由于我懒，接下来就以椭圆为例进行证明，其中过程涉及隐函数求导。

证明：

给定椭圆 b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 及其上一点 P(x0,y0)P(x_{0},y_{0}) ，记过 PP 的切线为 ll 。

对椭圆标准方程两边同时求导，即进行隐函数求导，得 2xa2+2y·y′b2=0\frac{2x}{a^2}+\frac{2y·y}{b^2}=0

整理并代入 P(x0,y0)P(x_{0},y_{0}) 得 kl=−b2x0a2y0k_{l}=-\frac{b^2x_{0}}{a^2y_{0}}

将斜率代入点斜式方程得 y−y0=−b2x0a2y0(x−x0)y-y_{0}=-\frac{b^2x_{0}}{a^2y_{0}}(x-x_{0})

整理一下就会有 ll 的方程 x0xa2+y0yb2=1\frac{x_{0}x}{a^2}+\frac{y_{0}y}{b^2}=1

2.角平分线定理

定理：

给定任意 △ABC\triangle ABC , ADAD 为其一条角平分线，如图。

则有 ABAC=BDCD\frac{AB}{AC}=\frac{BD}{CD} 。

其实这个应该在初中就学过了，不过鉴于部分同学可能忘记，就补充说明一下。这个证明是极为简单的。

证明：

过 DD 分别作 、AB、ACAB、AC 边的垂线 、DE、DFDE、DF ，如图所示。

由角平分线的性质可知， DE=DFDE=DF 。

一方面， S△ABDS△ACD=BD×hCD×h=BDCD\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{BD\times h}{CD\times h}=\frac{BD}{CD}

另一方面， S△ABDS△ACD=AB×DEAC×DF=ABAC\frac{S_{\triangle ABD}}{S_{\triangle ACD}}=\frac{AB\times DE}{AC\times DF}=\frac{AB}{AC}

所以有 ABAC=BDCD\frac{AB}{AC}=\frac{BD}{CD} ，另外可以注意到，其逆定理也成立。

3.光学性质

结论：

①从椭圆的一个焦点射出光线，光线碰到椭圆边界反射后的路径经过另一个焦点。如图。

②从双曲线的一个焦点射出光线，光线碰到双曲线边界反射后的路径的反向延长线经过另一个焦点。如图。

③从抛物线的焦点射出光线，光线碰到抛物线边界反射后的路径平行于抛物线的对称轴。如图。

4.椭圆的光学性质证明

给定椭圆 b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 及其上一点 P(x0,y0)P(x_{0},y_{0}) ，且 、F1、F2F_{1}、F_{2} 分别为椭圆的左右焦点。现有一束光线从 F1F_{1} 射出，在点 PP 处反射经过 F2F_{2} 。

法一（常规方法）：

其实主要还是采用验证的方法，也就是先假设光线反射后会经过 F2F_{2} ，然后通过角平分线定理的逆定理说明这就是光线的路径。

首先作出过 PP 的切线 ll ，然后过 PP 作 ll 的垂线交 F1F2F_{1}F_{2} 于 QQ ，如图所示。

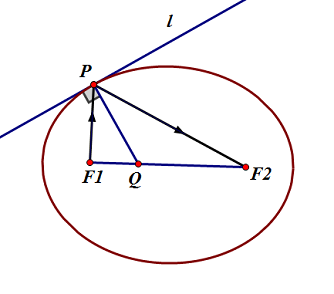
若 PF2PF_{2} 就是光线反射后的路径，那由物理知识可知，应有 ∠F1PQ=∠F2PQ\angle F_{1}PQ=\angle F_{2}PQ

而由角平分线定理就有 PF1PF2=F1QF2Q\frac{PF_{1}}{PF_{2}}=\frac{F_{1}Q}{F_{2}Q} ，这就是需要验证的等式

设椭圆的离心率为 ee ，由椭圆的第二定义可知， PF1PF2=a+ex0a−ex0\frac{PF_{1}}{PF_{2}}=\frac{a+ex_{0}}{a-ex_{0}}

另一方面，由配积定理可以得到 l:x0xa2+y0yb2=1l:\frac{x_{0}x}{a^2}+\frac{y_{0}y}{b^2}=1

由 kl×kPQ=−1k_{l}\times k_{PQ}=-1 同时也就能得到 PQ:y−y0=a2y0b2x0(x−x0)PQ:y-y_{0}=\frac{a^2y_{0}}{b^2x_{0}}(x-x_{0})

代入 y=0y=0 即可得到 Q(c2x0a2,0)Q(\frac{c^2x_{0}}{a^2},0)

故有 F1QF2Q=c+c2x0a2c−c2x0a2=a+ex0a−ex0=PF1PF2\frac{F_{1}Q}{F_{2}Q}=\frac{c+\frac{c^2x_{0}}{a^2}}{c-\frac{c^2x_{0}}{a^2}}=\frac{a+ex_{0}}{a-ex_{0}}=\frac{PF_{1}}{PF_{2}}

法二（希尔伯特同一法）：

同上先作出过 PP 的切线 ll ，然后作 F1F_{1} 关于 ll 的对称点 F′F ，连接 F′F2FF_{2} 交 ll 于 P′P ，如图所示。

接下来就是要说明 PP 和 P′P 为同一点。

首先由作图过程可知， P′P 为 ll 上使得 P′F1+P′F2PF_{1}+PF_{2} 最小的点。

然后又因为 ll 为过 PP 的切线，所以有 P′F1+P′F2≥PF1+PF2PF_{1}+PF_{2}\geq PF_{1}+PF_{2}

综上所述，即有 P′F1+P′F2=PF1+PF2PF_{1}+PF_{2}=PF_{1}+PF_{2} ，即 PP 与 P′P 重合。

因此， PF2PF_{2} 就是光线反射后的路径。

这种证明方法很美。希尔伯特果然很强。

然后因为双曲线的光学性质的证明方法也是大同小异，这里就不赘述了。

5.抛物线的光学性质证明

给定抛物线 0)">y2=2px(x>0)y^2=2px(x>0) 及其上一点 P(x0,y0)P(x_{0},y_{0}) ，且 FF 为抛物线的焦点。现有一束光线从 FF 处射出，在点 PP 处反射后的轨迹与 xx 轴平行。

证明：

作出过 PP 的切线 ll 和过 PP 的光线反射轨迹 l′l ，如图所示。

由作图过程知， ∠1=∠2\angle 1=\angle 2 。

由配积定理知， l:y0y=px0+pxl:y_{0}y=px_{0}+px

代入 y=0y=0 得 Q(−x0,0)Q(-x_{0},0) ，即 |FQ|=p2+x0|FQ|=\frac{p}{2}+x_{0}

由抛物线的第二定义可知 |PF|=p2+x0=|QF||PF|=\frac{p}{2}+x_{0}=|QF|

所以有 ∠3=∠2=∠1\angle3=\angle2=\angle1 ，亦即 l′//l//xx 轴。

应用(Application)

1.给定椭圆 b>0)">x2a2+y2b2=1(a>b>0)\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) 及其上一动点 PP ， ll 为过 PP 的切线， F′F 为椭圆其中一个焦点 FF 在 ll 上的投影，则 F′F 的运动轨迹为 x2+y2=a2x^2+y^2=a^2 。如图。

证明：

首先作 FF 关于 ll 的对称点 F1F_{1} ，连接 、、F1F0、PF、OF′F_{1}F_{0}、PF、OF ，如图。

由椭圆的光学性质可知， PP 在 F1F0F_{1}F_{0} 上。

又易知 OF′OF 为 △F0F1F\triangle F_{0}F_{1}F 的中位线，所以有 OF′=12F0F1=12(PF0+PF)=aOF=\frac{1}{2}F_{0}F_{1}=\frac{1}{2}(PF_{0}+PF)=a

即 F′F 到坐标原点 OO 的距离为定值 aa ，所以 F′F 的轨迹方程为 x2+y2=a2x^2+y^2=a^2

尾言(The last)

写这篇文耗时最长的竟然是画图……画切线实在是有点麻烦。其实笔者对于光学性质也不太熟，没有做深入研究，因此也不能举出很好的应用例子，深感抱歉。这篇文主要还是想给各位读者欣赏一下圆锥曲线光学性质证明方法之美，特别是我很喜欢的希尔伯特同一法，十分优雅。

最后附上王尔德的一句话：

不要虚掷你的黄金时代，不要去倾听枯燥乏味的东西，

不要设法挽留无望的失败，不要把你的生命献给无知、平庸和低俗。

健康食品 产品推荐 洗护测评 知识科普