【圆锥曲线】圆锥曲线解题瘦身计划（4）光学性质&四个圆

一，前言

前三篇文章基本涵盖了圆锥曲线的特殊情况简化方法和常见模型组合的射影背景及其翻译。本文我们最后再来介绍一下圆锥曲线中常考的几个特殊情况，这几个构型以几何性质较为初等的几个圆为核心衍生题目，即外准圆又称蒙日圆，内准圆，外辅助圆，内辅助圆。

这几个特殊的初等几何构型除蒙日圆和内准圆在模考中涉及比较多以外，剩余两个相关圆仍然处于偶尔涉及一次的冷门频率。从扫盲汇集的角度来看，我们仍然需要对它们的性质进行一定程度的了解。了解这几个圆本身需要涉及一点光学性质，所以对光学性质，本文也会略有涉及。

这几个圆在几何和代数的角度分别可以从斜率和角度的定值进行推广，这目前还未进行过高考的考察，但鉴于新高考可能的灵活化，这里的推广也会一并给出。

没有看过前几篇文章的可以进行了解。

二，模型介绍

1，光学性质

从焦点射出的光线经椭圆/双曲线反射后的光线在的直线过另一焦点，抛物线的反射光线则平行于轴。如图所示

光学性质的等价表述是

入射和出射光组成的角被这一处的切线和法线平分，这里的平分包括内角的平分和外角的平分。

光学性质的证明可以直接从光路最短得到几何的启发直接证明。

对于椭圆

假设 F1F_1 关于切线 ll 对称点 F′F 不在 AF2AF_2 上，那么设 F2F′∩l=A′F_2F\cap l=A’ ，由两点之间线段最短， ＜A′F2+A′F′=A′F2+A′F1＜AF2+AF1AF_2+AF=AF_2+AF_1＜AF_2+AF_1 ，而 A′A 在椭圆外，故由椭圆定义矛盾， F′F’ 在 AF2AF_2 直线上，即证。

由椭圆启发，双曲线是类似的。

假设 F1F_1 关于切线 ll 对称点 F′F 不在 AF2AF_2 上，那么设 F2F′∩l=A′F_2F\cap l=A’ ，由三角形的线段长关系， ＞|A′F2−A′F′|=|A′F2−A′F1|＞|AF2−AF1|=|AF2−AF′|\left| AF_2-AF \right|=\left| AF_2-AF_1 \right|＞\left| AF_2-AF_1 \right|=\left| AF_2-AF \right| ，而 A′A 在双曲线外，故由双曲线定义矛盾（ aa 越小双曲线越向中部移动）， F′F’ 在 AF2AF_2 直线上，即证。

类似的辅助线用在抛物线上

因为抛物线只有一个焦点，所以考虑转化证明 FF′⊥ACFF\bot AC ，因为等腰三角形 AF′FAFF 的三线合一中垂直最容易代数证明。

抛物线 y2=2pxy^2=2px 上一点 A(2pt2,2pt)A\left( 2pt^2,2pt \right) 和过它的直线 ：l：2pty=p(x+2pt2)l：2pty=p\left( x+2pt^2 \right) 联立后 Δ=0\Delta=0 为切线，其在准线的投影 F′(−p2,2pt)F\left( -\dfrac{p}{2},2pt \right) , FF′FF 中点 ，C(0，pt)=l∩yC\left( 0，pt \right)=l\cap y 轴，抛物线定义 |AF′|=|AF|\left| AF’ \right|=\left| AF \right| 三线合一， ll 是角平分线，故得证。

有的地方将平行轴直线视为抛物线所谓 xx 轴上第二个焦点在无穷远处，这只能算辅助记忆，但它本身没有一点道理，是完全错的

光学性质是非退化二次曲线重要且基本的几何性质，几个圆的研究需要基于光学性质展开。

2，外准圆（蒙日圆）

外准圆的证明有代数和几何数种，代数上主要是利用斜率，从 k1k2=−1k_1k_2=-1 的角度分析

但是这样实际上就失去了处理角度的能力，所以这里先介绍几何法方便下面几节分析

之后在 66 部分里再讲一讲代数的证明方法。

希望处理角度那就需要从纯几何入手最为方便，如以下两种辅助线组

分别处理双曲线椭圆，抛物线

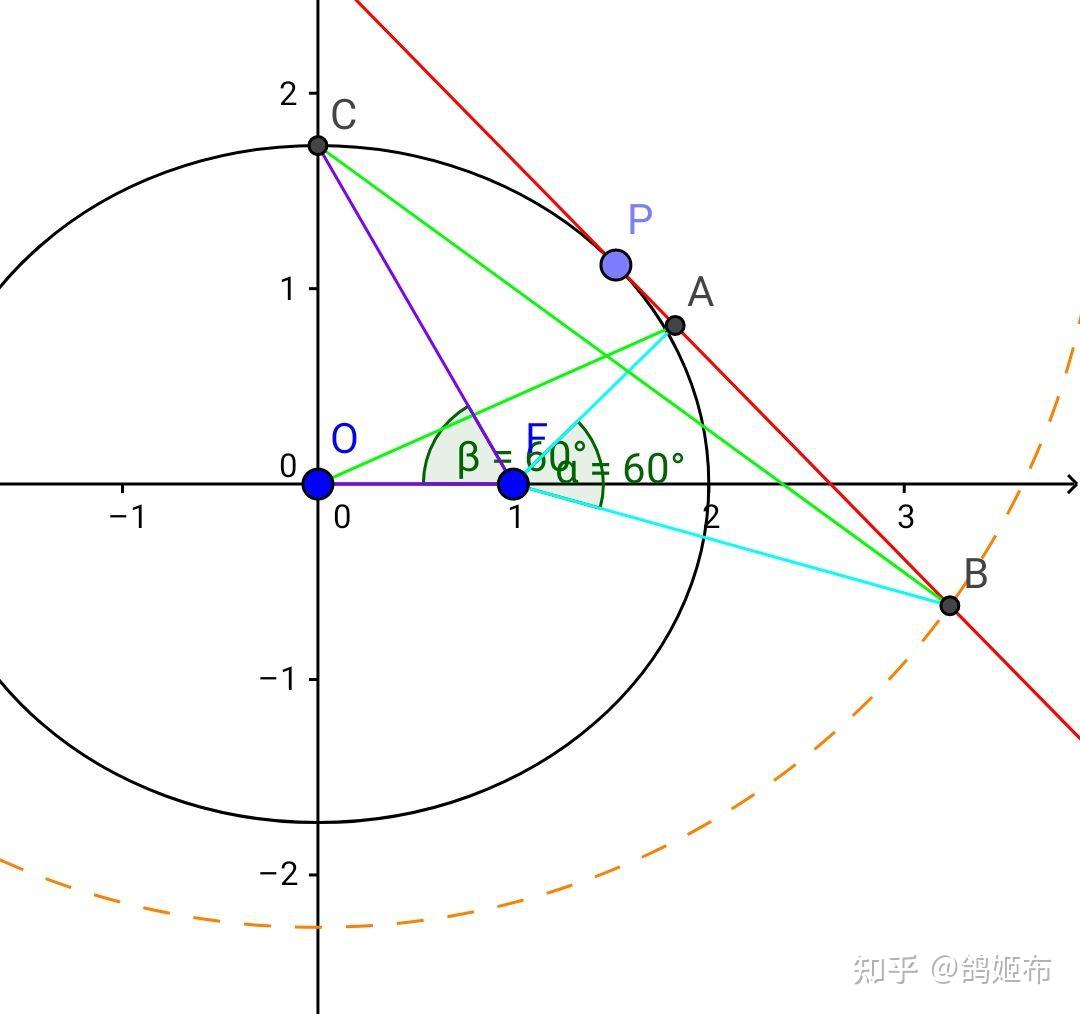
上述辅助线组虽然复杂，但是历史悠久，同时具有强大的解决力，只要这一套线组还能同时解决6模型里的数个延申性质。

假设 F1F_1 关于切线 PAPA 对称点 F1′F_1 不在 AF2AF_2 上，那么设 F2F1′∩PA=A″F_2F_1\cap PA=A’ ，由两点之间线段最短， ＜A″F2+A″F1′=A″F2+A″F1＜AF2+AF1AF_2+AF_1=AF_2+AF_1＜AF_2+AF_1 ，而 A″A 在椭圆外，故由椭圆定义矛盾， F1′F_1’ 在 AF2AF_2 直线上所以同理 AP,BPAP,BP 是 F1F1′,F2F2′F_1F_1,F_2F_2 中垂线，因而 F1′F2=F2′F1=2a,PF1=PF1′,PF2=PF2′F_1F_2=F_2F_1=2a,PF_1=PF_1,PF_2=PF_2

那么 ΔPF1′F2≃ΔPF1F2′(SSS)\Delta PF_1F_2 \simeq \Delta PF_1F_2\left( SSS \right) ， ∠F1′PF2=∠F1PF2′∠F_1PF_2=∠F_1PF_2 ，且 ∠APB=90°∠APB=90°那么∠F1′PA=∠F1PA=∠F2′PB=∠F2PB∠F_1PA=∠F_1PA=∠F_2PB=∠F_2PB 有 ∠F1′PF2=∠F1PF2′=90°∠F_1PF_2=∠F_1PF_2=90°

那么 F1′P2+F2P2=F1P2+F2P2=F1′F22=4a2F_1P^2+F_2P^2=F_1P^2+F_2P^2=F_1F_2^2=4a^2

所以 ΔPF1F2\Delta PF_1F_2 中线长定理有 PP 轨迹是以 OO 为圆心，半径 a2+b2\sqrt{a^2+b^2} 的圆

这对辅助线高度通用，对双曲线也是相似的

假设 F1F_1 关于切线 PAPA 对称点 F1′F_1’ 不在 AF2AF_2 上，那么设 F2F1′∩PA=A″F_2F_1\cap PA=A’ ，由三角形的线段长关系， ＞|A″F2−A″F1′|=|A″F2−A″F1|＞|AF2−AF1|=|AF2−AF1′|\left| AF_2-AF_1 \right|=\left| AF_2-AF_1 \right|＞\left| AF_2-AF_1 \right|=\left| AF_2-AF_1 \right| ，而 A″A 在双曲线外，故由双曲线定义矛盾， F1′F_1 在 AF2AF_2 直线上，所以 同理AP,BPAP,BP 是 F1F1′,F2F2′F_1F_1,F_2F_2 中垂线，因而 F1′F2=F2′F1=2aF_1F_2=F_2F_1=2a

且 F1′F2=F2′F1=2a,PF1=PF1′,PF2=PF2′F_1F_2=F_2F_1=2a,PF_1=PF_1,PF_2=PF_2 ，那么 ΔPF1′F2≃ΔPF1F2′(SSS)\Delta PF_1F_2 \simeq \Delta PF_1F_2\left( SSS \right) ， ∠F1′PF2=∠F1PF2′∠F_1PF_2=∠F_1PF_2 ，且 ∠APB=90°∠APB=90°那么∠F1′PA=∠F1PA=∠F2′PB=∠F2PB∠F_1PA=∠F_1PA=∠F_2PB=∠F_2PB 有 ∠F1′PF2=∠F1PF2′=90°∠F_1PF_2=∠F_1PF_2=90°

那么 F1′P2+F2P2=F1P2+F2P2=F1′F22=4a2F_1P^2+F_2P^2=F_1P^2+F_2P^2=F_1F_2^2=4a^2

所以 ΔPF1F2\Delta PF_1F_2 中线长定理有 PP 轨迹是以 OO 为圆心，半径 a2−b2\sqrt{a^2-b^2} 的圆

这里可以看出，双曲线的蒙日圆并非一定存在，而是需要保证实轴线段长大于虚轴线段长，因而上面步骤一开始还需要一句“当轨迹存在时”作为前提

上面的几何关系在变化过程中是恒成立的，如图

对于抛物线，我们熟知交点弦两端切线交准线于同一点且夹角直角，所以方向是证明轨迹是准线

这里我们用第二种辅助线组，即阿基米德三角形的辅助线组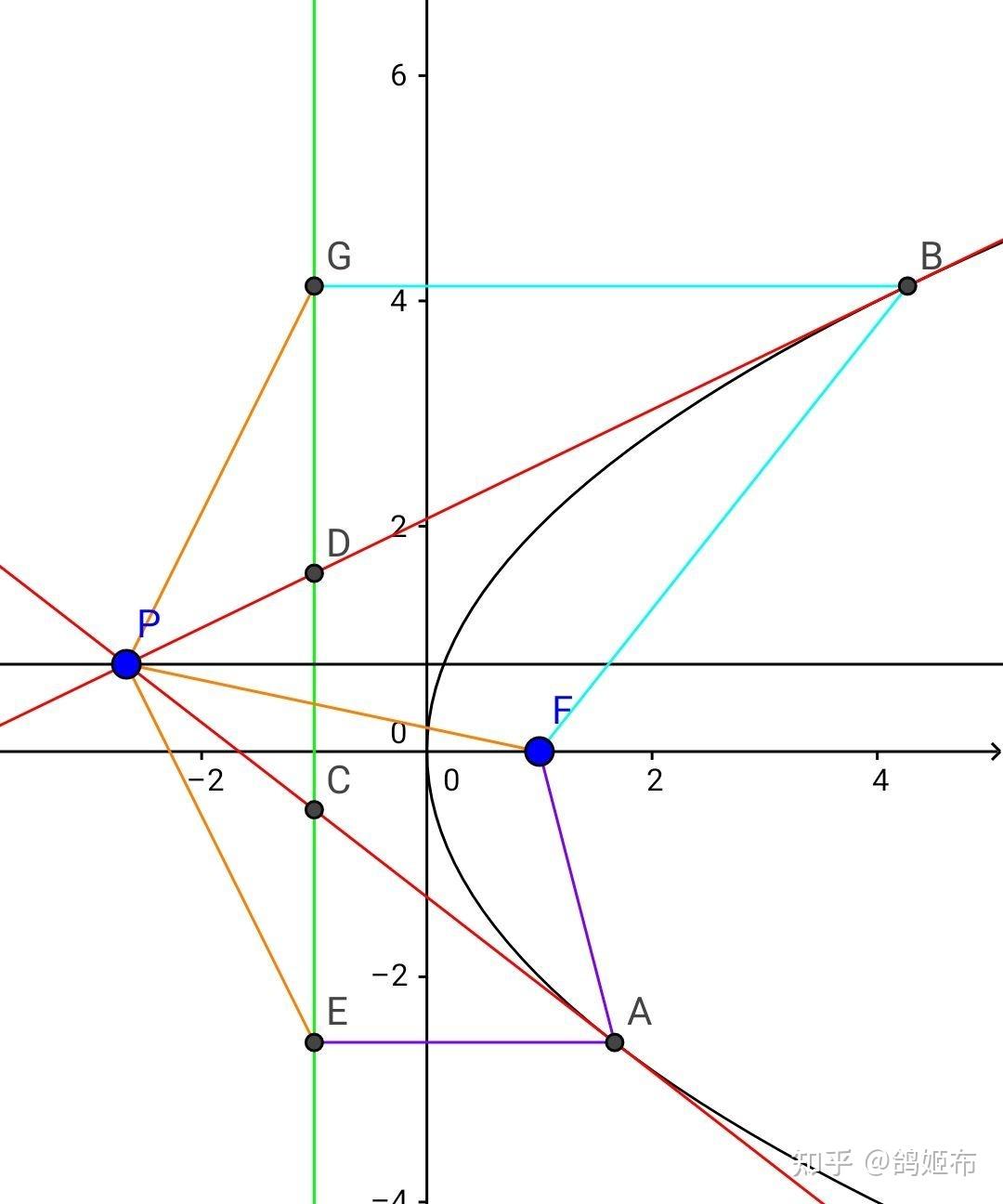

抛物线 y^2=2px 上一点 A\left( 2pt^2,2pt \right) 和过它的直线 l：2pty=p\left( x+2pt^2 \right) 联立后 \Delta=0 为切线，其在准线的投影 E\left( -\dfrac{p}{2},2pt \right) , FE 中点 S\left( 0，pt \right)=l\cap y 轴，抛物线定义 \left| AE \right|=\left| AF \right| 三线合一， l 是 ∠EAF 角平分线， B 处切线同理，那么 SAS 有 \Delta PBG\simeq\Delta PBF 和 \Delta PAE\simeq\Delta PAF

全等有PG=PF=PE ,和 \left| cos2∠BPA \right|=\left| cos∠GPE \right| ，过 P 做准线的垂线 \alpha其也是角平分线 ，则 P 到 F 和到准线距离之比为 \left| \dfrac{1}{cos∠BPA} \right| ，所以非直角时 P 轨迹是双曲线一部分，直角时重合于准线

这个图形表述也是恒成立的

在某一定角时，轨迹只能取到双曲线中的一支，另一支在补角时取

这时候还能顺便用 ∠PEA=∠PGB=∠PFA=∠PFB=90° 得到 AB 过 F 点，这其实就是 P 在 F 极线上时 P 的极线 AB 也过 F

这一配极原则的体现

有的地方将这里的准线视为半径无穷大的圆以和前两个外准圆统一，但事实上从推导过程只有抛物线角度在非直角时仍导出二次曲线来看，强行统一也没什么实在的意义

3，内准圆

内准圆被认为是非退化二次曲线中心 O 和一弦 l 两交点连线 OA\bot OB 时

AB 的包络曲线的轨迹，这也是目前高考唯几个考的包络

因为抛物线中心在无穷远点，所以 OA∥OB ，因而实平面内不可能有垂直

所以它没有内准圆，就只要看椭圆和双曲线的情况

内准圆在几何上要由外准圆通过配极变换得到，这对于高考就有些多余了

且椭圆双曲线配极会得知非直角的其他定角包络不是二次曲线

就只剩下了斜率之积非 -1 情况的拓展，这是代数的

因而这里其实使用齐次化要更胜一筹

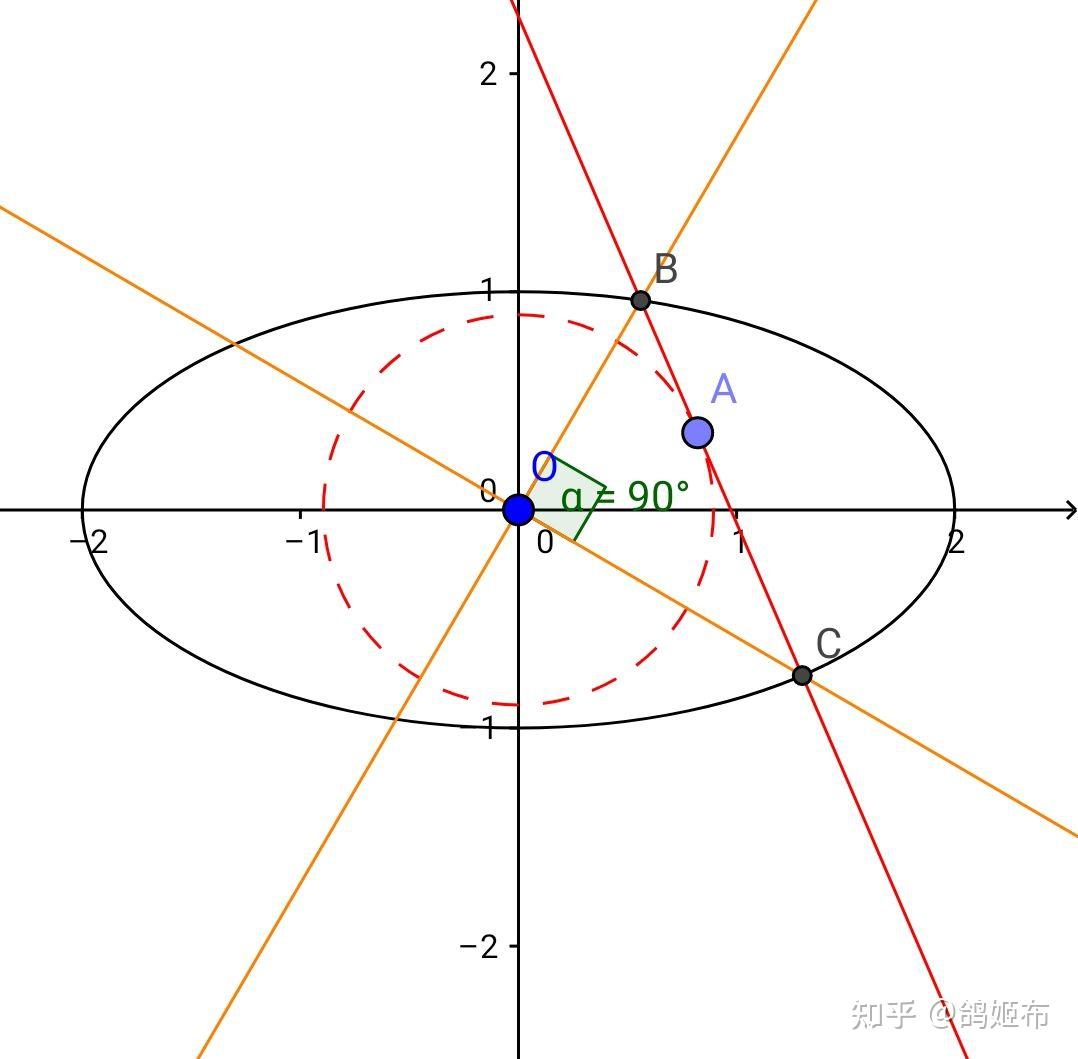
如图中心在原点的椭圆 \Gamma:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 ,有不过原点的直线 l：mx+ny=1 ， l\cap\Gamma=B,C

齐次化联立 b^2x^2+a^2y^2=a^2b^2\left( mx+ny \right)^2 , \Delta ＞0 同除 x^2 , k_{OB},k_{OC}=k_1,k_2=\dfrac{y}{x}

a^2\left( b^2n^2-1 \right)k^2+2mna^2b^2k+b^2\left( a^2m^2-1 \right)=0,k_1k_2=-1

韦达定理有 m^2+n^2=\dfrac{1}{a^2}+\dfrac{1}{b^2} ,代入 O，l 距离方程知距离 L=\dfrac{\left| ab \right|}{\sqrt{a^2+b^2}}

所以 l 恒包络圆 x^2+y^2=\dfrac{a^2b^2}{a^2+b^2} ,这个圆就是内准圆

双曲线是类似的

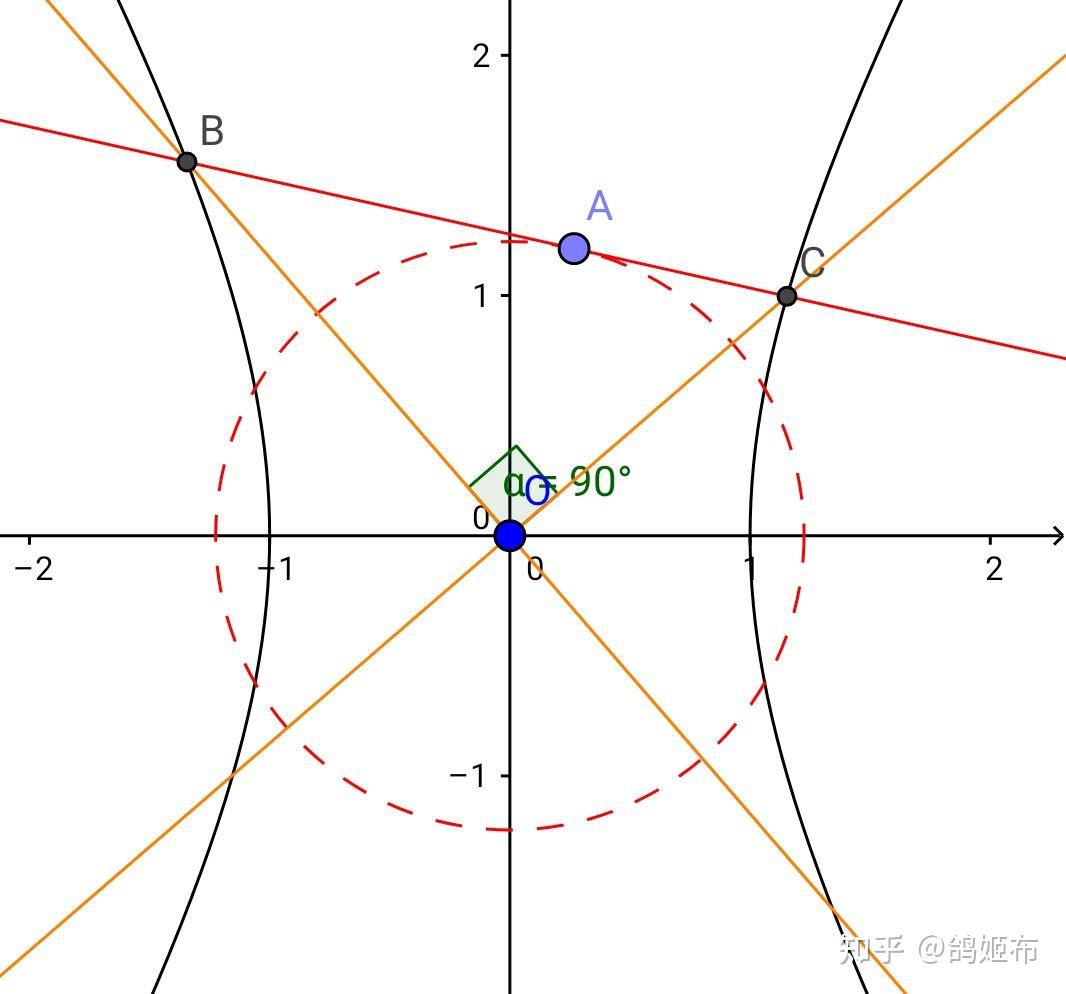
如图中心在原点的双曲线 \Gamma:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 ,有不过原点的直线 l：mx+ny=1 ， l\cap\Gamma=B,C

齐次化联立 b^2x^2-a^2y^2=a^2b^2\left( mx+ny \right)^2 , \Delta ＞0 同除 x^2 , k_{OB},k_{OC}=k_1,k_2=\dfrac{y}{x}

a^2\left( b^2n^2+1 \right)k^2+2mna^2b^2k+b^2\left( a^2m^2-1 \right)=0,k_1k_2=-1

韦达定理有 m^2+n^2=\dfrac{1}{a^2}-\dfrac{1}{b^2} ,代入 O，l 距离方程知距离 L=\dfrac{\left| ab \right|}{\sqrt{b^2-a^2}}

所以 l 恒包络圆 x^2+y^2=\dfrac{a^2b^2}{b^2-a^2}

这里也能看出双曲线的内准圆和外准圆至多存在一个

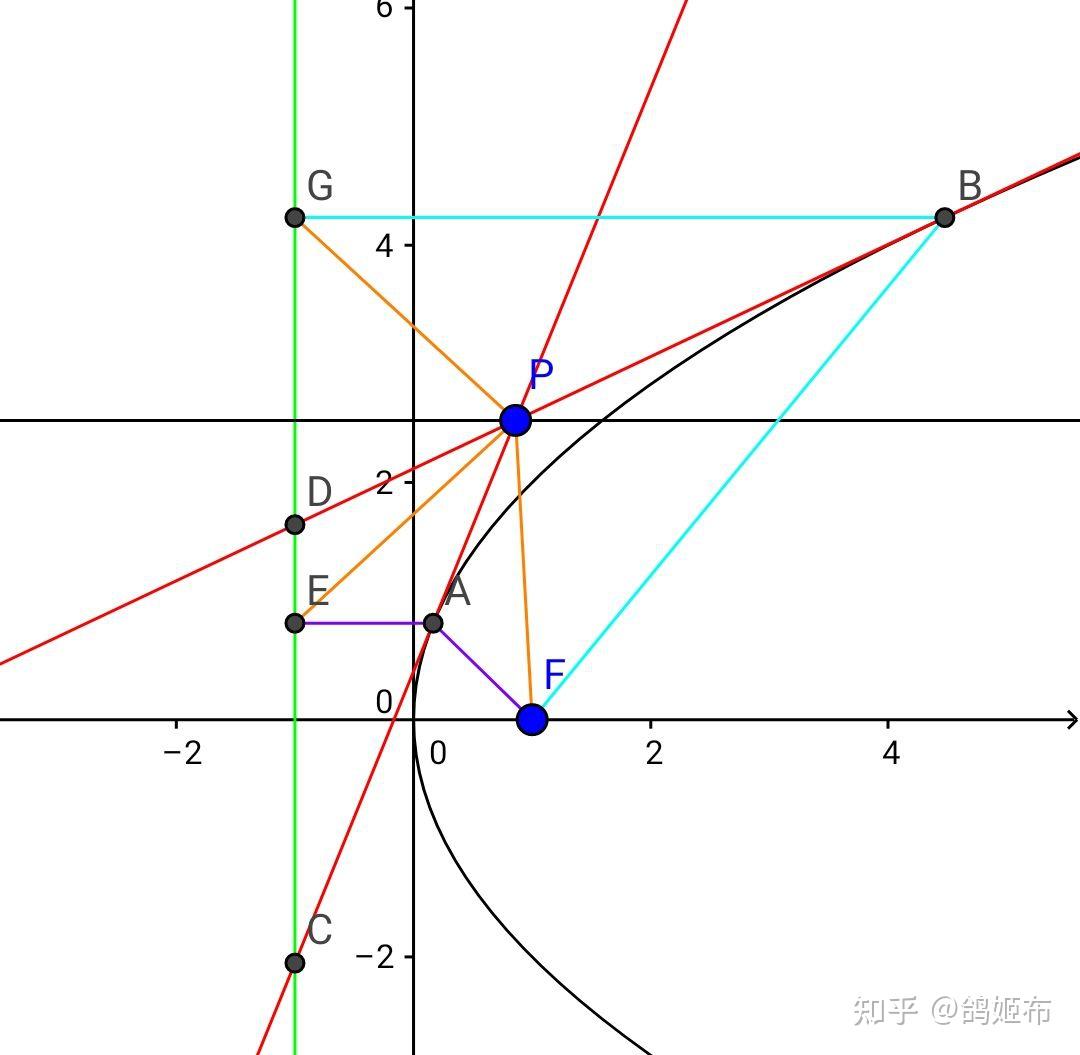
4，外辅助圆

外辅助圆是焦点引出直线和切线垂直的垂足轨迹

这个轨迹直接由光学性质引出，且可以推广，我们在 6 模型中给出推广

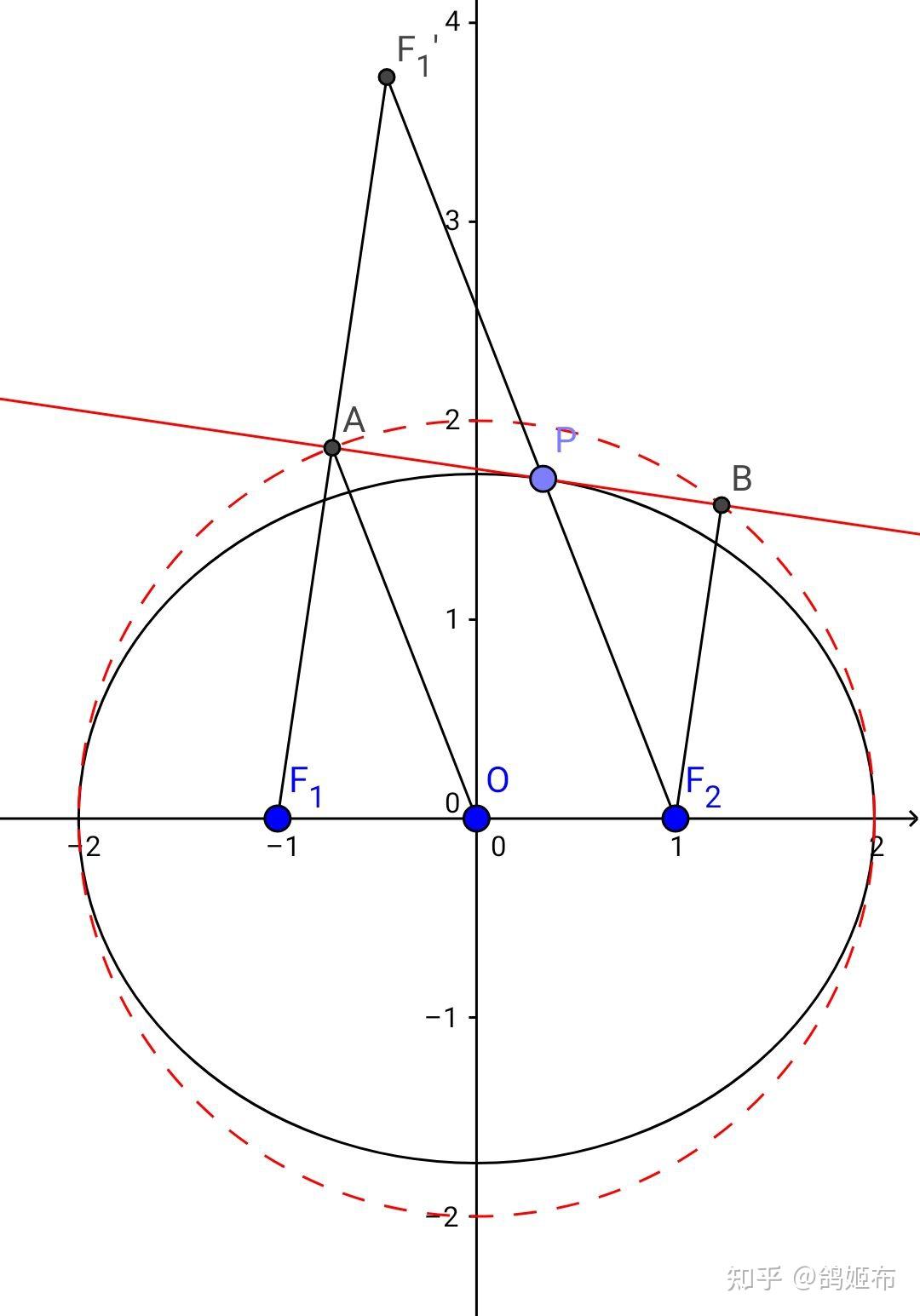
如图假设 F_1 关于切线 l 对称点 F_1 不在 PF_2 上，那么设 F_2F_1\cap l=P’ ，由两点之间线段最短， PF_2+PF_1=PF_2+PF_1＜PF_2+PF_1 ，而 P 在椭圆外，故由椭圆定义矛盾， F_1’ 在 PF_2 直线上故 F_1F_2=2a ， AO 是 \Delta F_1F_1F_2 中位线所以 AO=a 故 A,B 都在圆 x^2+y^2=a^2 上

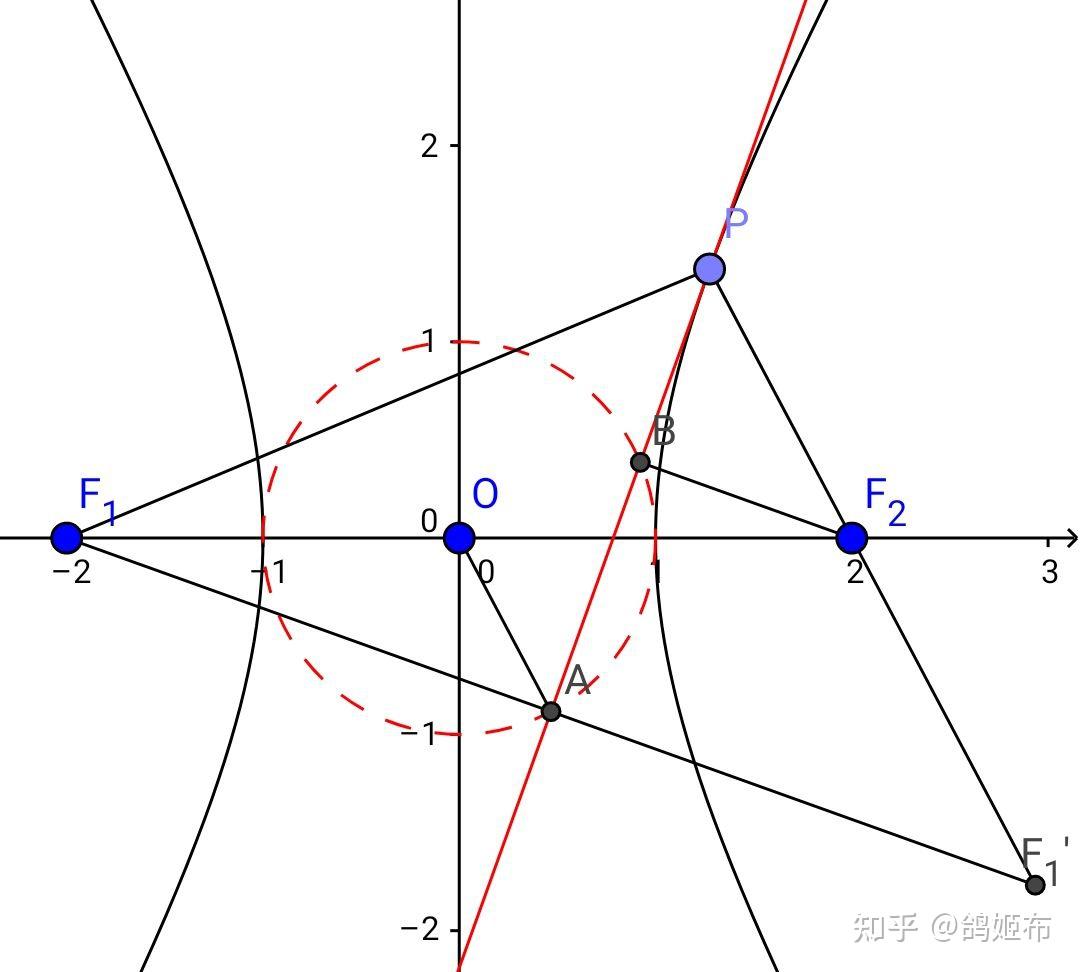
如图假设 F_1 关于切线 l 对称点 F_1 不在 PF_2 上，那么设 F_2F_1\cap l=P’ ，由三角长度关系， \left| PF_2-PF_1 \right|=\left| PF_2-PF_1 \right|＞\left| PF_2-PF_1 \right|=\left| PF_2-PF_1 \right| ，而 P 在双曲线外，故由双曲线定义矛盾， F_1 在 PF_2 直线上故 F_1F_2=2a ， AO 是 \Delta F_1F_1F_2 中位线所以 AO=a 故 A,B 都在圆 x^2+y^2=a^2 上

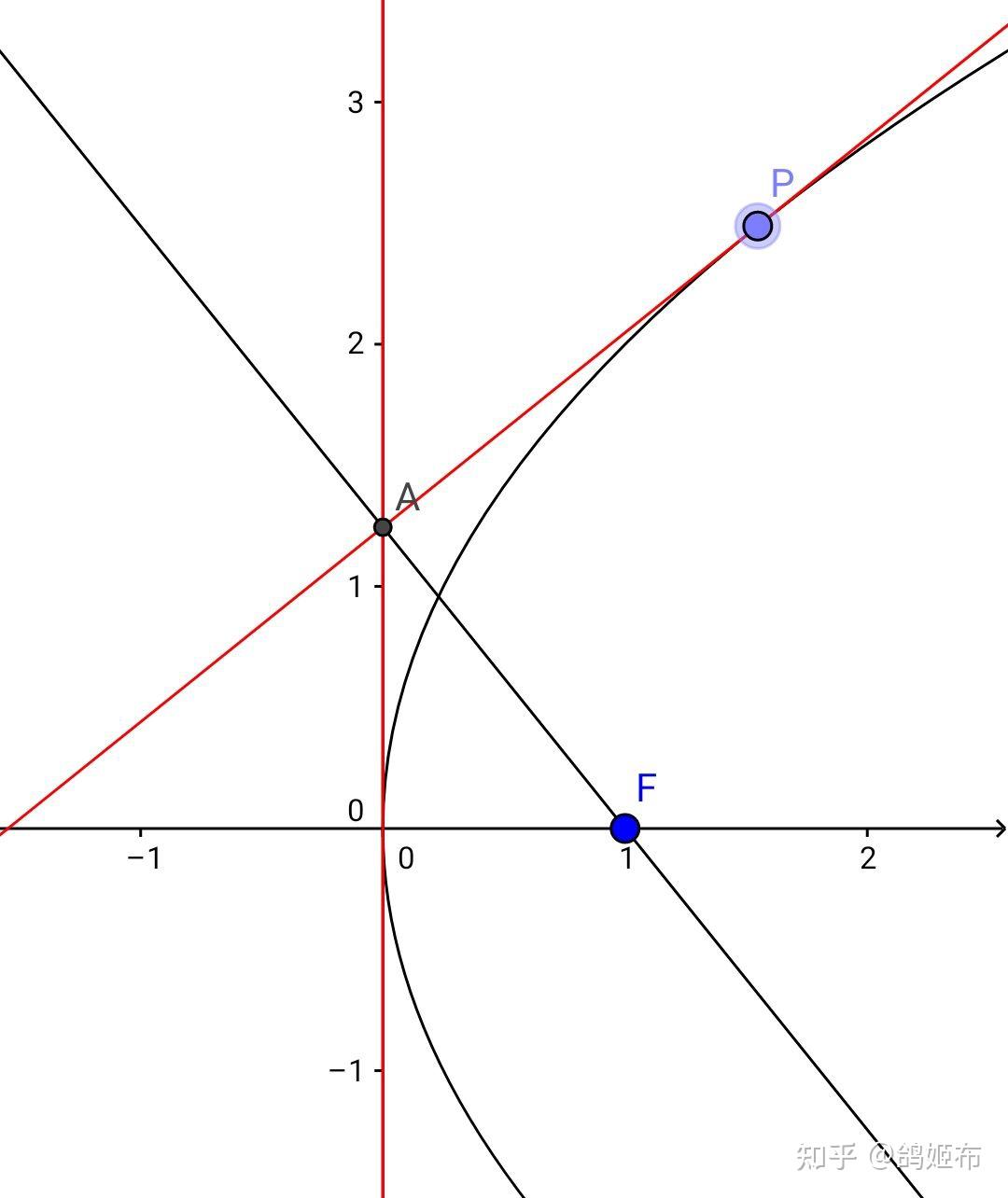
抛物线 y^2=2px 上一点 P\left( 2pt^2,2pt \right) 和过它的直线 l：2pty=p\left( x+2pt^2 \right) 联立后 \Delta=0 为切线， A\left( 0，pt \right)=l\cap y 轴， \overrightarrow{AP}·\overrightarrow{FA}=\left( 2pt^2,pt \right)·\left( -\dfrac{p}{2}，pt \right)=0 故轨迹是 y 轴

5，内辅助圆

内辅助圆和外辅助圆相对，外辅助圆切于长轴/实轴端点

那对应的切于短轴/虚轴的圆就叫内辅助圆

内辅助圆性质比较零散，这里只做列举

首先是斜率和相等的性质，这是内辅助圆下面三个性质里唯一椭圆和双曲线都成立的性质

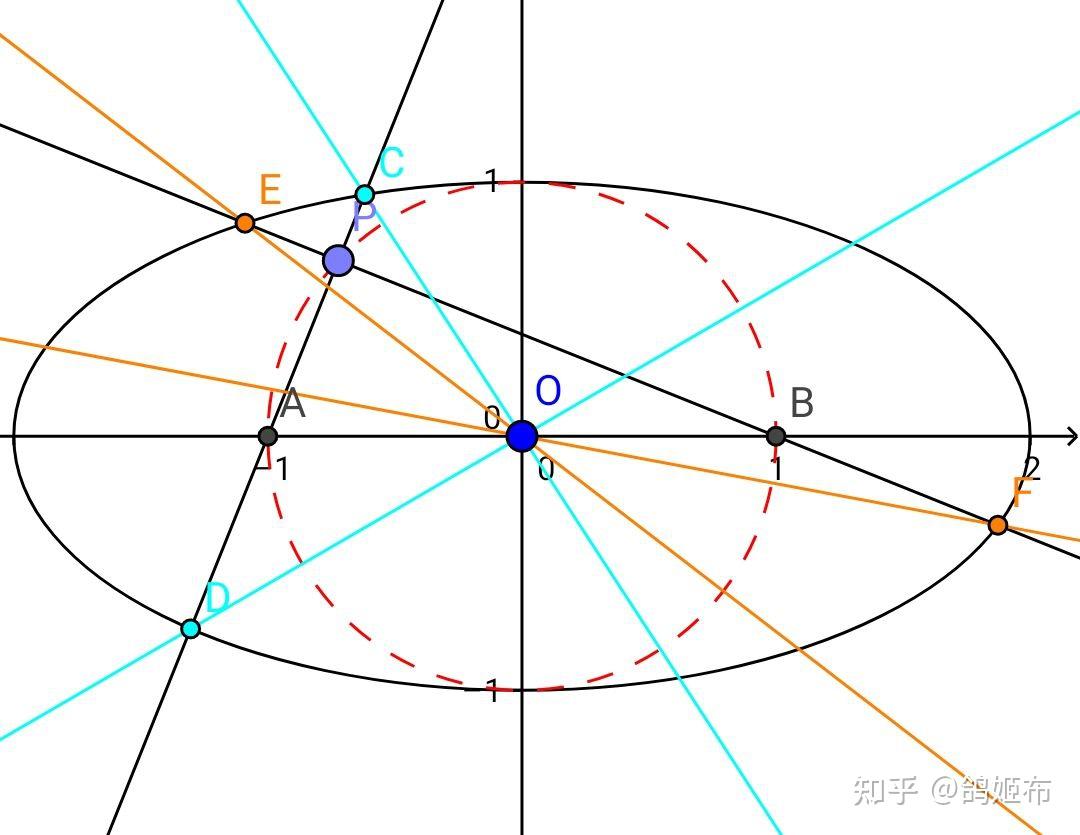
如图 P 在内辅助圆上，长轴和圆交点 A,B 和 P 连出两条线， PB\cap \Gamma=E,F , PA\cap \Gamma=C,D

那么 k_{OC}+k_{OD}=k_{OE}+k_{OF} 恒成立

这个性质用齐次化表述非常容易证明，且可以拓展

这里只做列举，证明拓展放到 6 部分中进行

这个性质对双曲线也成立

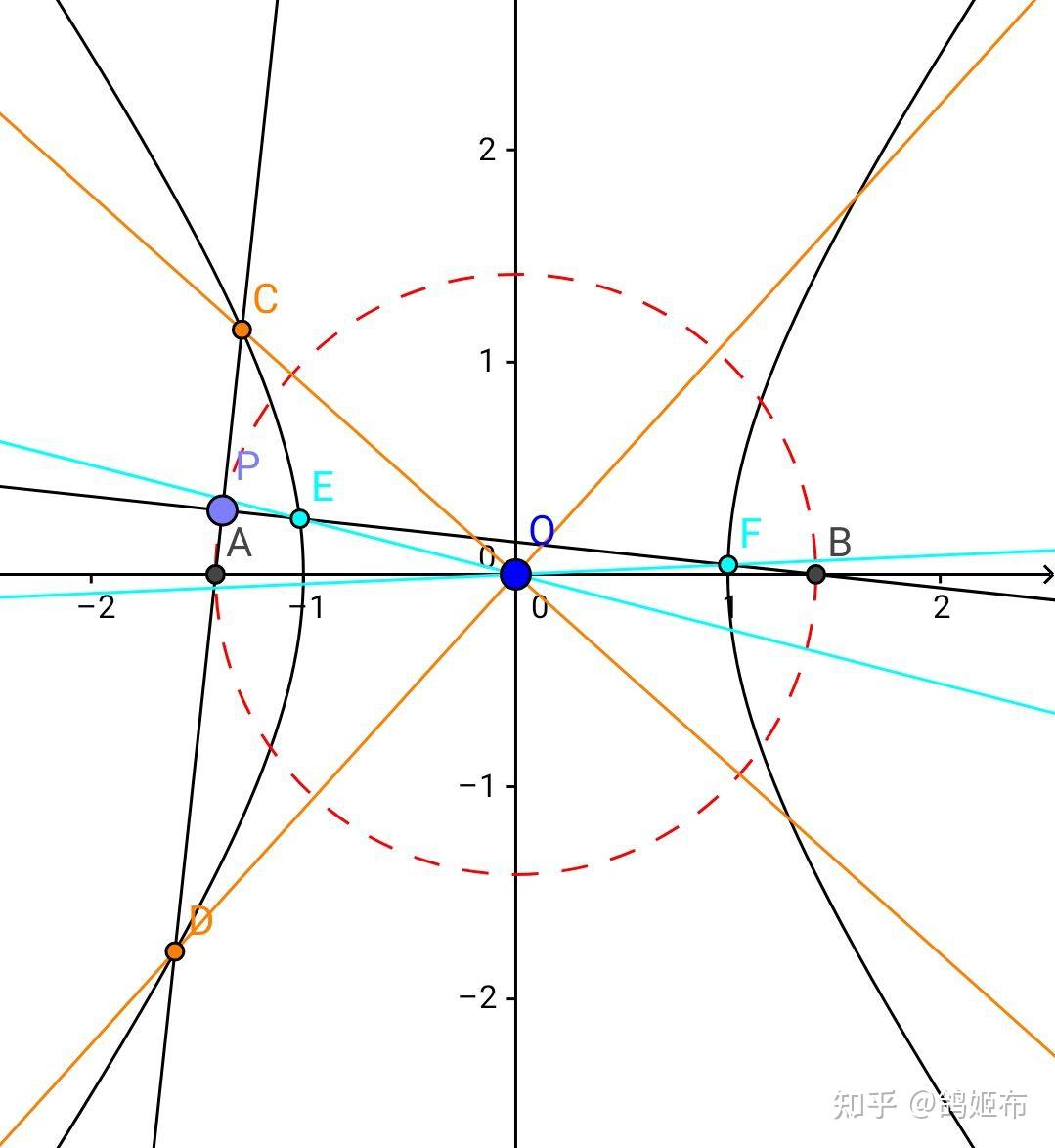
然后是一组交点的轨迹在直线上的性质

如图，若有 PA 切内辅助圆且交椭圆于 A ，过 O 做 OA 的垂线交 AP 于 B ，那么 B 的轨迹是两条直线的并集，这两条直线可以表示为 y^2=\dfrac{a^2b^2}{a^2-b^2} ，这和内准圆有点像

这个性质只在椭圆的内辅助圆适用，本质是由外辅助圆的定义做外辅助圆的配极得到

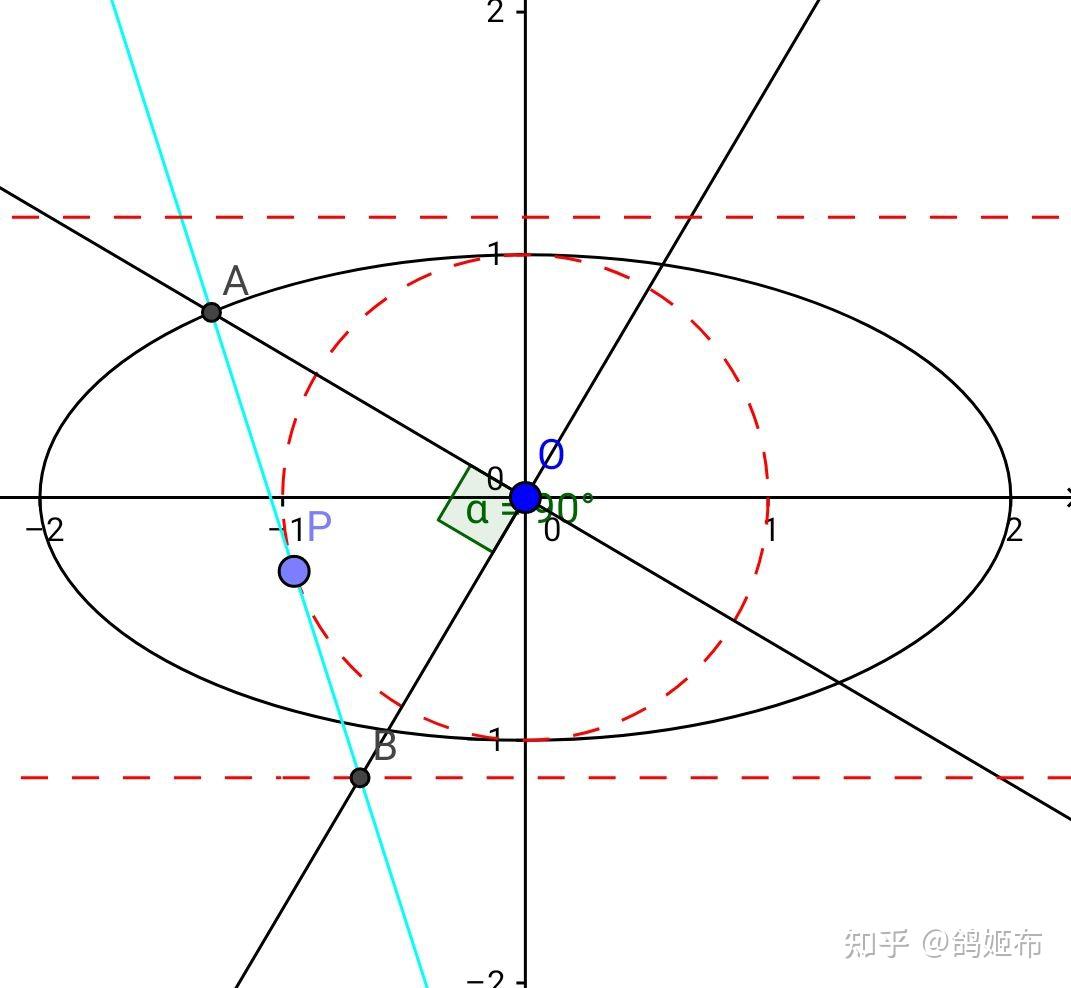
除上面两个性质，这里还有一个非常冷门的长度性质

这里也只做罗列

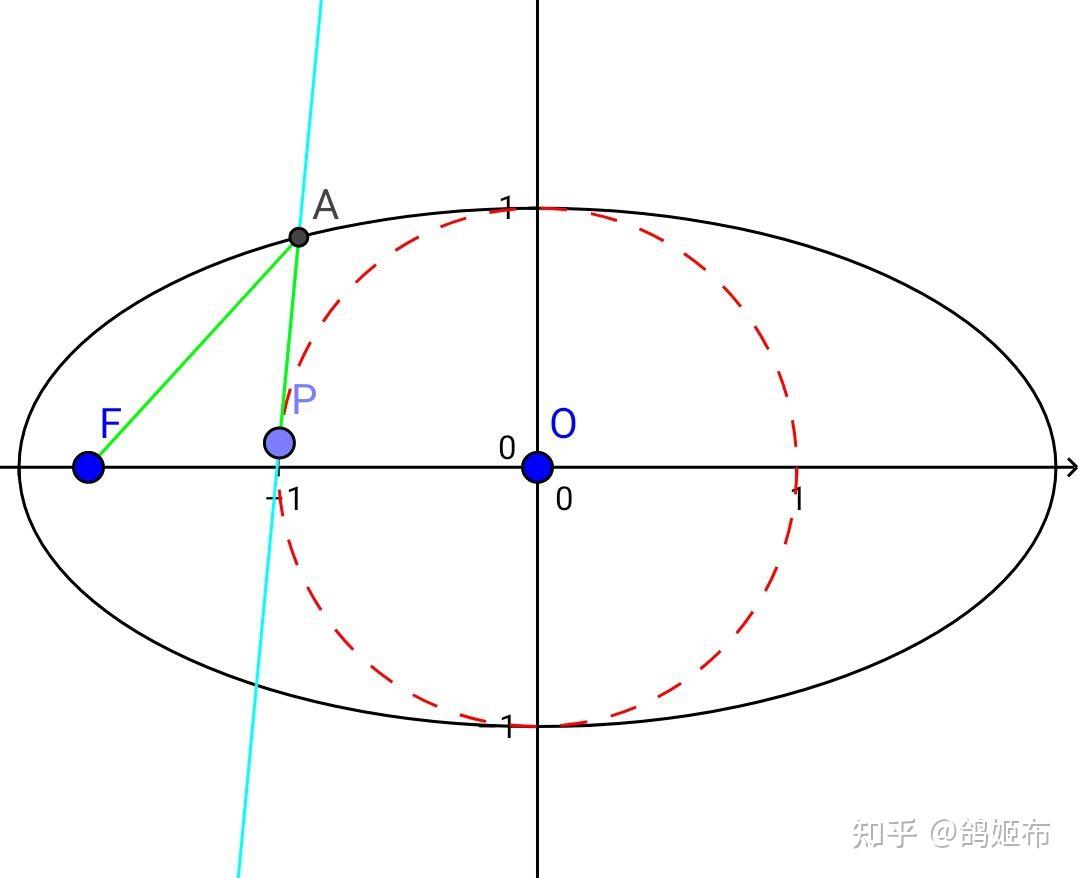
PA 切内辅助圆且交椭圆于 A ，连接 A 与 PA 同侧的焦点 F ，则 AF+AP 为定值

这个定值为半长轴长 a

如果设 PA 交椭圆的另一个点为 B 则 \Delta FAB 周长恒为 2a

这个性质只做罗列，因为考的可能性着实不大

6，斜率/角度定值类衍生

在这里我们对外准圆，内准圆，外辅助圆，内辅助圆可以拓展的斜率/角度关系进行拓展

有兴趣的读者自己选取部分阅读

外准圆的角度拓展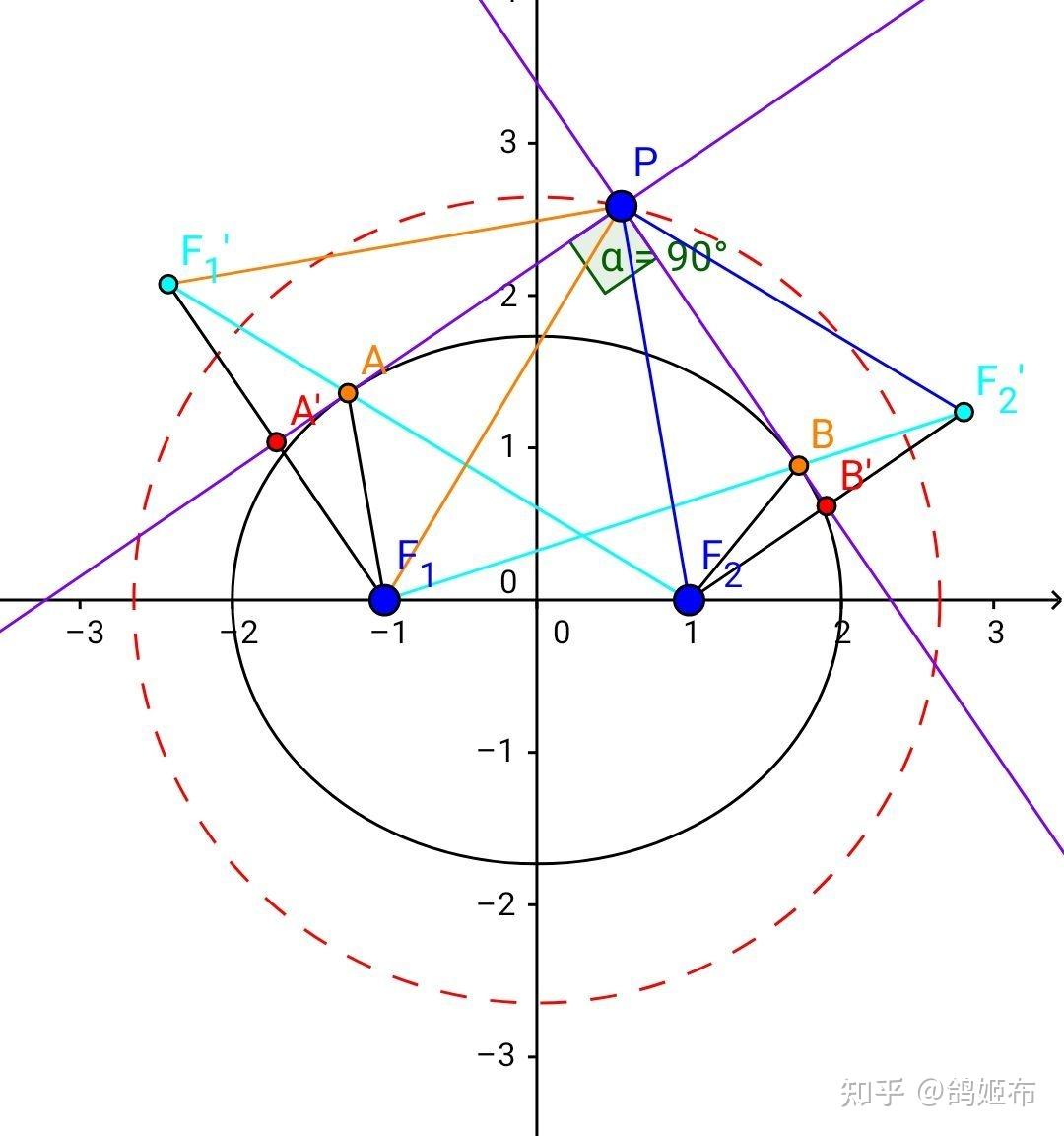之前说了这组辅助线大有作用，那我们就接着之前的步骤来看看还有什么可拓展。

首先是两切线夹角 ∠APB 为任意定角时的轨迹，这大约算一种科普。

已经有 \Delta PF_1F_2 \simeq \Delta PF_1F_2\left( SSS \right) ， ∠F_1PF_2=∠F_1PF_2 ，且 ∠APB=\alpha那么∠F_1PA=∠F_1PA=∠F_2PB=∠F_2PB 有 ∠F_1PF_2=∠F_1PF_2=\alpha

那么余弦定理 F_1P^2+F_2P^2-2F_1P·F_2Pcos\alpha=F_1F_2^2

全等即 F_1P^2+F_2P^2-2F_1P·F_2Pcos\alpha=4a^2

设 P\left( x,y \right),F_1\left( -c,0 \right),F_2\left( c,0 \right) ,即可知其一般是一条四次曲线

直角时退化为蒙日圆，平角时就是椭圆本身

这个结论代表着内准圆和外准圆在角度拓展是不能出题的

这个思路方向就可以舍弃，看到这种钓鱼题也可以不用管

这对双曲线也是相似的，而抛物线则不同，轨迹是二次曲线中的双曲线

除此之外，还有一组用的到的性质考试时常涉及，需要介绍。

先介绍焦点的等角性质，在上一篇文章的 2 部分中我们曾经提到

记二次曲线存在的任意焦点为 F_1 ，二次曲线外的一点 A 做出两条切线切于 B,C ， F_1 准线为 l BC\cap l=D ， AF_1\cap BC =E， CF_1\cap l=G 那么这里有三个结论 I ∠BF_1A=∠CF_1A II ∠GF_1D=∠BF_1D III DF_1\bot AF_1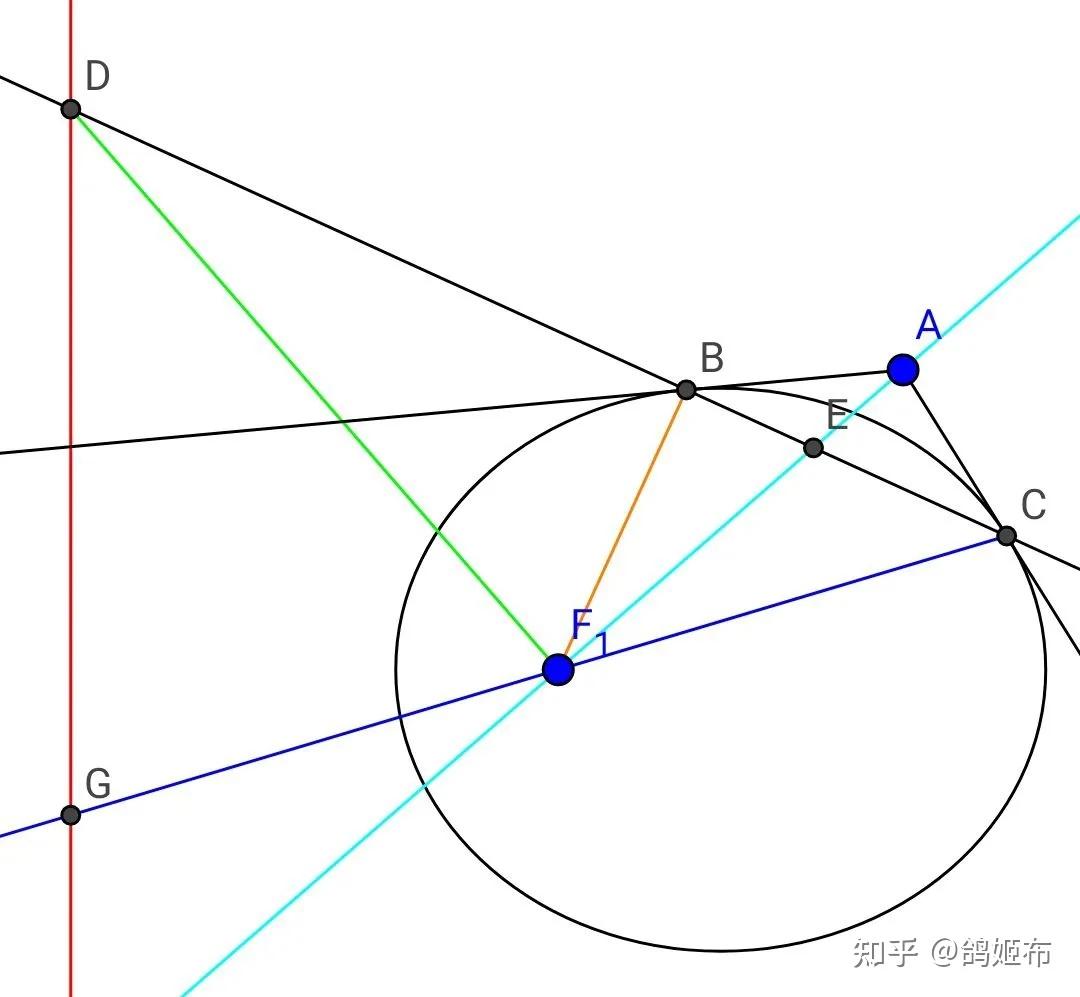

之前我们证明了第二个结论，这里我们就把之一个结论的等角也证明一下，当之一和第二个结论都证明时由内外角平分线垂直自然就证明了第三个结论。

如图， A,B 是切点的情况下 ∠AF_1P=∠BF_1P , ∠AF_2P=∠BF_2P

这个性质在这个辅助线下是显然的因为已经有 \Delta PF_1F_2 \simeq \Delta PF_1F_2\left( SSS \right)

且 AP,BP 是 F_1F_1,F_2F_2 中垂线，那么 ∠AF_1P=∠AF_1P=∠BF_1P

F_2 情况同理 ∠PF_2B=∠PF_2B=∠PF_2A

这个性质对双曲线，抛物线也是成立的，双曲线完全一样，这里提一下抛物线

现在有 \Delta PBG\simeq\Delta PBF 和 \Delta PAE\simeq\Delta PAF全等有PG=PF=PE 有等腰三角

那么 ∠PEC=∠PGD ，再加直角就是 ∠PEA=∠PGB ，全等过去就是 ∠PFA=∠PFB

最后再介绍一下彭赛列小定理

上图为例，这个定理的内容就是 ∠APF_1=∠BPF_2

根据 \Delta PF_1F_2 \simeq \Delta PF_1F_2\left( SSS \right) ， ∠F_1PF_2=∠F_1PF_2 ，那么配合中垂线∠F_1PA=∠F_1PA=∠F_2PB=∠F_2PB 即证

小定理考察的概率不大，只做知识面拓展就行

外准圆的斜率拓展

通过蒙日圆直角的 k_1k_2=-1 情况，我们仿射就能得到 k_1k_2=n 的任意情况

这个简单的结论我们就直接给出了，满足切线之积为 n 的点 P

在 \Gamma：\dfrac{x^2}{a^2}\pm\dfrac{y^2}{b^2}=1 时，方程为 \dfrac{x^2}{a^2\mp \dfrac{b^2}{n}}-\dfrac{y^2}{a^2·n\mp b^2}=1

请注意 \pm 和 \mp 的不同

事实上，在几何中这由内准圆的配极导出会更加简单和显然

但是我们这里就只能用代数来推导 k_1+k_2=m 的推广了

这里先给出结论 \Gamma：\dfrac{x^2}{a^2}\pm\dfrac{y^2}{b^2}=1 外 P 做两切线满足 k_1+k_2=m

则 P 的轨迹是 {2xy}=m\left( x^2-a^2 \right)

以下是椭圆的推导过程，首先我们知道两切线的切点连线是极线

而 P\left( x_0,y_0 \right) 对 \Gamma 的极线是 l：\dfrac{xx_0}{a^2}+\dfrac{yy_0}{b^2}=1 ,若将 P 平移至原点

将极线对应成齐次化里 mx+ny=1 那么 k_1,k_2 的韦达就能用齐次化表达，如图

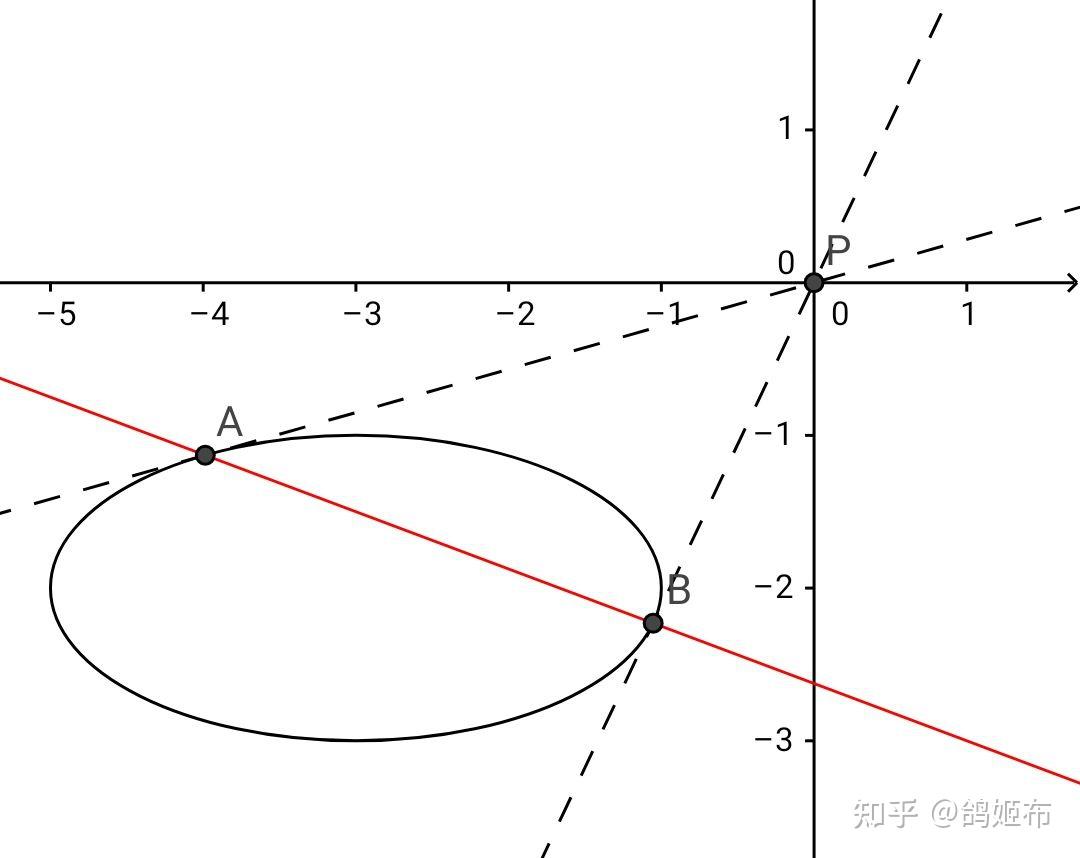
这里平移后 \Gamma：\dfrac{\left( x+x_0 \right)^2}{a^2}+\dfrac{\left( y+y_0 \right)^2}{b^2}=1 , l：\dfrac{\left( x+x_0 \right)x_0}{a^2}+\dfrac{\left( y+y_0 \right)y_0}{b^2}=1

把 l 写成 mx+ny=1 的形式则 \left\{ \begin{aligned} &m=\dfrac{\frac{x_0}{a^2}}{1-\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}}\\ &n=\dfrac{\frac{y_0}{b^2}}{1-\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}} \end{aligned} \right. ，齐次化

\dfrac{ x^2+2x_0\left( mx+ny \right)x}{a^2}+\dfrac{y^2+2y_0\left( mx+ny\right)y}{b^2}=\left( 1-\dfrac{x_0^2}{a^2}-\dfrac{y_0^2}{b^2} \right)\left( mx+ny \right)^2

同除 x^2 化简为 ak^2+bk+c=0 则 \left\{ \begin{aligned} &a=\dfrac{2y_0n}{b^2}+\frac{1}{b^2}+\left( \dfrac{x_0^2}{a^2}+\dfrac{y_0^2}{b^2}-1 \right)n^2\\ &b=\dfrac{2x_0n}{a^2}+\dfrac{2y_0m}{b^2}+\left( \dfrac{x_0^2}{a^2}+\dfrac{y_0^2}{b^2}-1 \right)·2mn\end{aligned} \right.

直接韦达会很麻烦，我们先令 a=b=1 ，椭圆就变成了单位圆，得到结论再仿射

单位圆后 k_1+k_2=m=-\dfrac{b}{a}=\dfrac{2mn\left( 1-\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2} \right)-\frac{2y_0m}{b^2}-\frac{2x_0n}{a^2}}{\frac{2y_0n}{b^2}+\frac{1}{b^2}+\left( \frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}-1 \right)n^2}

代入 \left\{ \begin{aligned} &m=\dfrac{\frac{x_0}{a^2}}{1-\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}}\\ &n=\dfrac{\frac{y_0}{b^2}}{1-\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}} \end{aligned} \right. 就有原式等价 \dfrac{-2x_0y_0\left( 1-x_0^2-y_0^2 \right)}{\left( 1-x_0^2 \right)\left( 1-x_0^2-y_0^2 \right)}=m

化简就是对 x^2+y^2=1 做切线斜率之和为 m 的 P 的轨迹 \dfrac{2xy}{x^2-1}=m

仿射成 \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 ，那么斜率之和变为 \dfrac{b}{a}m ，轨迹 \dfrac{2xy\dfrac{a}{b}}{x^2-a^2}=m

即 k_1+k_2=t 时，轨迹是 \dfrac{2xy}{x^2-a^2}=t

这个方法处理双曲线（或复仿射）同样可以得到这个方程

因而 \Gamma：\dfrac{x^2}{a^2}\pm\dfrac{y^2}{b^2}=1 外 P 做两切线满足 k_1+k_2=m

则 P 的轨迹是 {2xy}=m\left( x^2-a^2 \right)

相似的，把这个方法用于抛物线我们能得到对于抛物线 y^2=2px

P 引出切线斜率满足 k_1+k_2=m 时轨迹为 y=mx

满足 k_1k_2=n 时， P 的轨迹为 x=\dfrac{p}{2n} ，垂直就退化对应准线

内准圆的情况（ AB 交曲线于 A,B ， k_{OA},k_{OB} 间斜率成上述和积关系）相似

结论是包络圆锥曲线（恒相切）这里不赘述

外辅助圆角度拓展

首先我们不加证明的告诉读者：外辅助圆不可以做斜率拓展即 k_1k_2=a,a\ne-1

这一点读者可以作图验证，轨迹并非二次曲线

因而我们将探索的重心放在角度上

即探究过 P 的切线若和过焦点 F 的直线交于 B ， ∠PBF=\theta

P,B,F 按某种时针顺序排列， B 的轨迹

这时的轨迹是一个圆

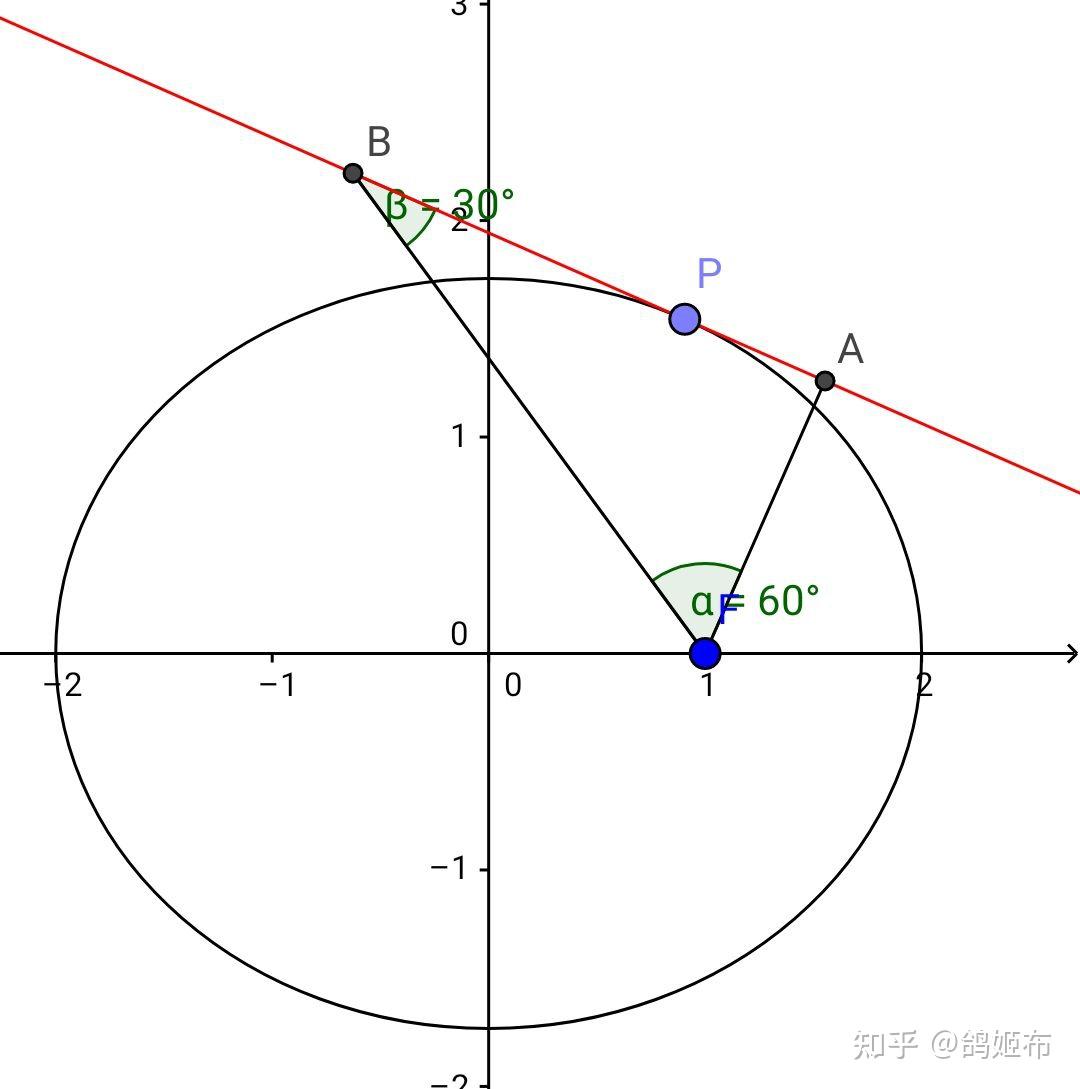
先探究 PBF 逆时针的情况，取垂直切线情况的垂足 A ，则 A 在外辅助圆上 ∠BFA=90°-\theta

做辅助线如图使得 ∠BFA=∠CFO=90°-\theta ，且均逆时针排列， C 在 y 轴上

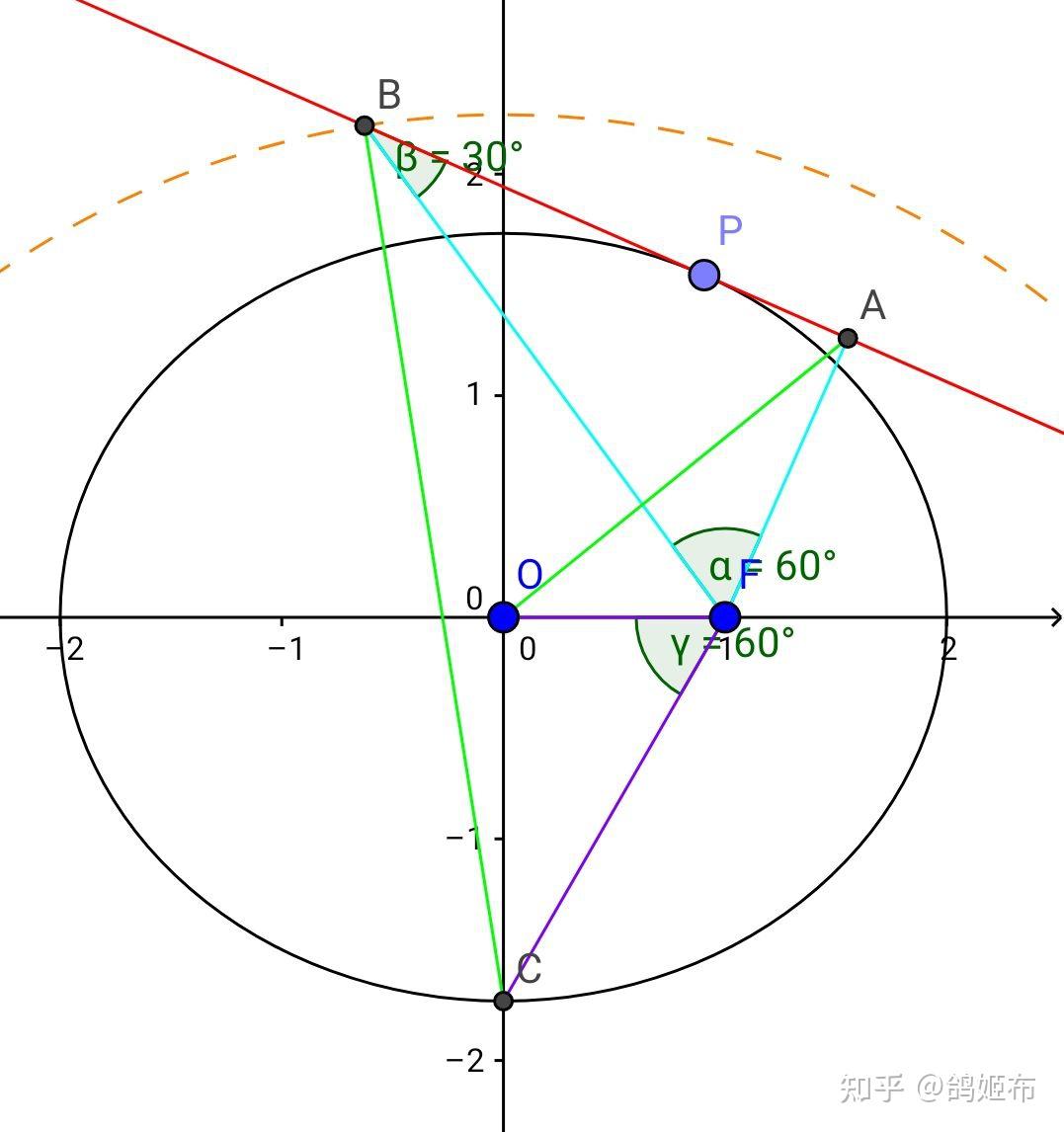
那么 \Delta COF\sim \Delta BAF ， \dfrac{FC}{FO}=\dfrac{BF}{FA} ， ∠BFA=∠CFO\Rightarrow∠CFB=∠OFA

因而 \Delta CFB\sim\Delta OFA ,且 \dfrac{FC}{FO}=\dfrac{CB}{OA}=\dfrac{1}{cos\left( 90°-\theta \right)} ，且外辅助圆 OA=a

故 CB=\dfrac{a}{cos\left( 90°-\theta \right)} ， C\left( 0，-c·tan\left( 90°-\theta \right) \right) 故B 轨迹是圆

顺时针排列其实没什么区别

相同的 \Delta COF\sim \Delta BAF ， \dfrac{FC}{FO}=\dfrac{BF}{FA} ， ∠BFA=∠CFO\Rightarrow∠CFB=∠OFA

因而 \Delta CFB\sim\Delta OFA ,且 \dfrac{FC}{FO}=\dfrac{CB}{OA}=\dfrac{1}{cos\left( 90°-\theta \right)} ，且外辅助圆 OA=a

故 CB=\dfrac{a}{cos\left( 90°-\theta \right)} ， C\left( 0，c·tan\left( 90°-\theta \right) \right) 故B 轨迹是圆

内辅助圆斜率拓展

在内辅助圆部分我们介绍了一条斜率和相等的性质，但没有说明是怎么得到的

事实上，通过下面的方法即可推广的得到斜率积相等，两和之和为 m 这样的各种拓展

这里给出斜率性质得证明，其余拓展请读者照葫芦画瓢

设 P\left( p,q \right) ， A\left( t,0 \right) ，那么设 AP：mx+ny=1 则 mt=1,mp+nq=1

即得 \left\{ \begin{aligned} &m=\frac{1}{t}\\ &n=\frac{t-p}{tq}\end{aligned} \right. ，齐次化联立，以椭圆为例就是 \Gamma :b^2x^2+a^2y^2=a^2b^2\left( mx+ny \right)^2

a^2\left( b^2n^2-1 \right)k^2+2mna^2b^2k+b^2\left( a^2m^2-1 \right)=0 , k_1+k_2=\dfrac{2mnb^2}{1-b^2n^2}=\dfrac{2b^2\frac{t-p}{qt^2}}{1-b^2\left( \frac{t-p}{qt} \right)^2}

若过 B\left( -t，0 \right) ， P 得直线和它斜率相等则 \dfrac{2b^2\frac{t-p}{qt^2}}{1-b^2\left( \frac{t-p}{qt} \right)^2}=\dfrac{2b^2\frac{-t-p}{qt^2}}{1-b^2\left( \frac{-t-p}{qt} \right)^2}

直接展开就是 b^2p^2+t^2q^2=t^2b^2 ,取 t=b 时即得证

这式子同时揭示了 t\ne b 时轨迹是椭圆

其余你们感兴趣得情况自己算

三，考题选赏

例一，炎德长郡中学2023月考2

之一题 \dfrac{x^2}{4}+\dfrac{y^2}{3}=1

显然，这矩形代表垂直，所以四点都在蒙日圆上，对角线长度就是两倍蒙日圆半径。

假设左焦点 F_1 关于切线 PA 对称点 F_1 不在右焦点连线 AF_2 上，那么设 F_2F_1\cap PA=A’ ，由两点之间线段最短， AF_2+AF_1=AF_2+AF_1＜AF_2+AF_1 ，而 A 在椭圆外，故由椭圆定义矛盾， F_1’ 在 AF_2 直线上所以同理 AP,BP 是 F_1F_1,F_2F_2 中垂线，因而 F_1F_2=F_2F_1=2a,PF_1=PF_1,PF_2=PF_2

那么 \Delta PF_1F_2 \simeq \Delta PF_1F_2\left( SSS \right) ， ∠F_1PF_2=∠F_1PF_2 ，且 ∠APB=90°那么∠F_1PA=∠F_1PA=∠F_2PB=∠F_2PB 有 ∠F_1PF_2=∠F_1PF_2=90°

那么 F_1P^2+F_2P^2=F_1P^2+F_2P^2=F_1F_2^2=4a^2

所以 \Delta PF_1F_2 中线长定理有 P 轨迹是以 O 为圆心，半径 \sqrt{a^2+b^2} 的圆

同理 M,N,P,Q 四点都在这个圆上，那么对角线长就是两倍得半径即 2\sqrt{7}

例二，北京2009高考理科

之一题 x^2-\dfrac{y^2}{2}=1

这题作为古代老题比较友善，直愣愣的考内准圆，可能是受年代和地区限制。

双曲线 \Gamma:{x^2}-\dfrac{y^2}{2}=1 ,有不过原点的直线 l：mx+ny=1 ， l\cap\Gamma=B,C

齐次化联立 2x^2-y^2=2\left( mx+ny \right)^2 , \Delta ＞0 同除 x^2 , k_{OB},k_{OC}=k_1,k_2=\dfrac{y}{x}

\left( 2n^2+1 \right)k^2+4mnk+2\left( m^2-1 \right)=0,k_1k_2=-1

韦达定理有 m^2+n^2=\dfrac{1}{2} ,代入 O，l 距离方程知距离 L=\dfrac{\left| ab \right|}{\sqrt{b^2-a^2}}

所以 l 恒包络圆 x^2+y^2=2 因而逆得 k_1k_2=-1 有 ∠AOB=90°

例三，2020湖南师大附中月考这一题固然可以平移齐次化，但这里我们试试用上述四圆来解决这个角

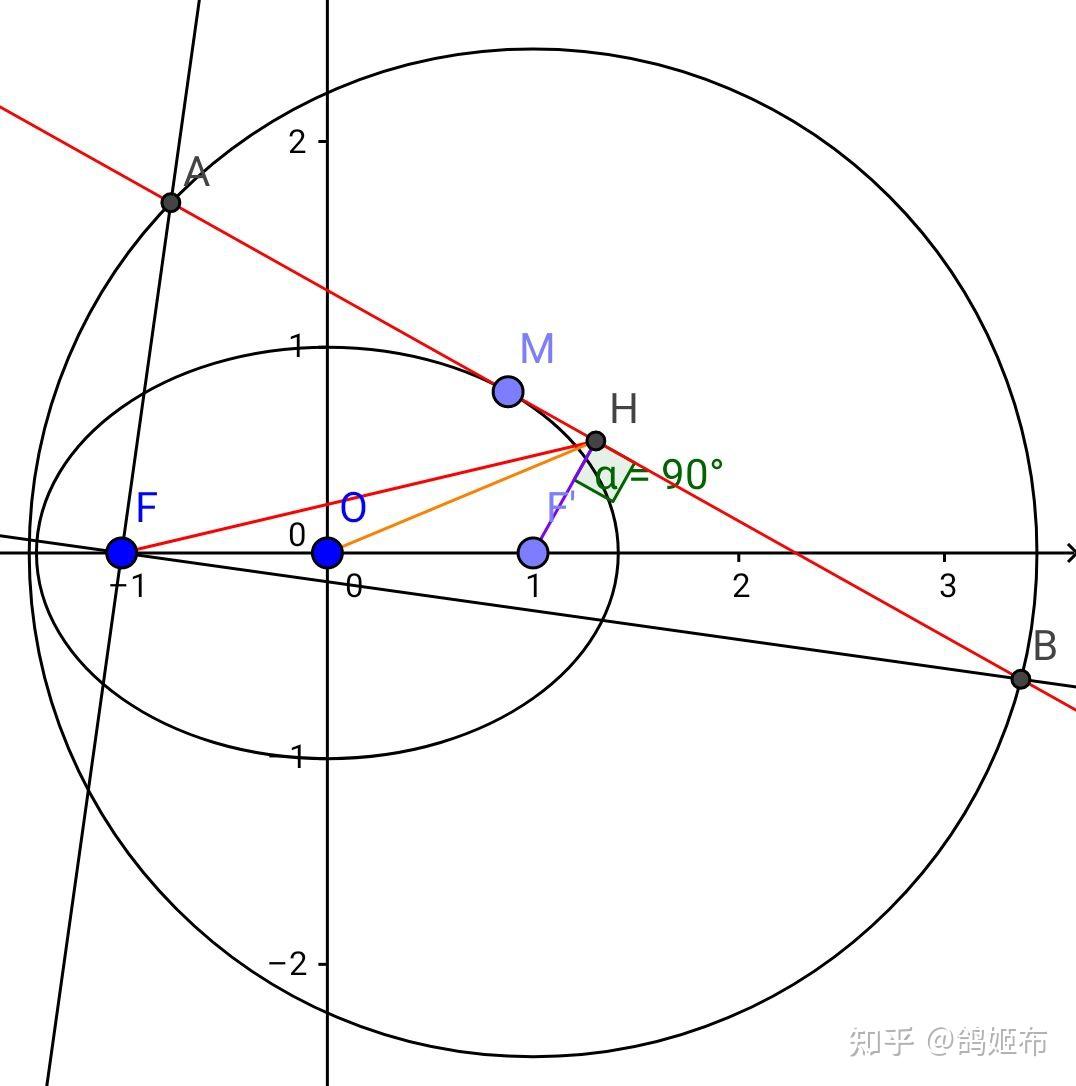
如图，我们做过圆心得切线得垂线，垂足是 H ，那么垂径定理， H 是中点

要证直角，只需要证 AH=HB=HF 即可

连接 FH,OH ,假设 F 关于切线 l 对称点 F 不在 MF 上，那么设 FF\cap l=M’ ，由两点之间线段最短， MF+MF=MF+MF＜MF+MF ，而 M 在椭圆外，故由椭圆定义矛盾， F’ 在 MF 直线上故 FF=2\sqrt{2} ， HO 是 \Delta FFF 中位线所以 HO=\sqrt{2}

对 \Delta FHF 使用中线长定理知 FH^2=6-FH^2 ,而垂径定理 HA^2=HB^2=6-FH^2

所以 AH=HB=HF ，所求恒为直角

例四，福建漳州2022之一次质量检测

之一题 \dfrac{x^2}{3}-y^2=1

第二题是非共线得长度比，这基本不会是纯射影得到的，这时候要先考虑光学性质和四个圆做辅助线。当然这题问的比较简单，直接代数也是可以得，之后会给出一道基于这一题的改编。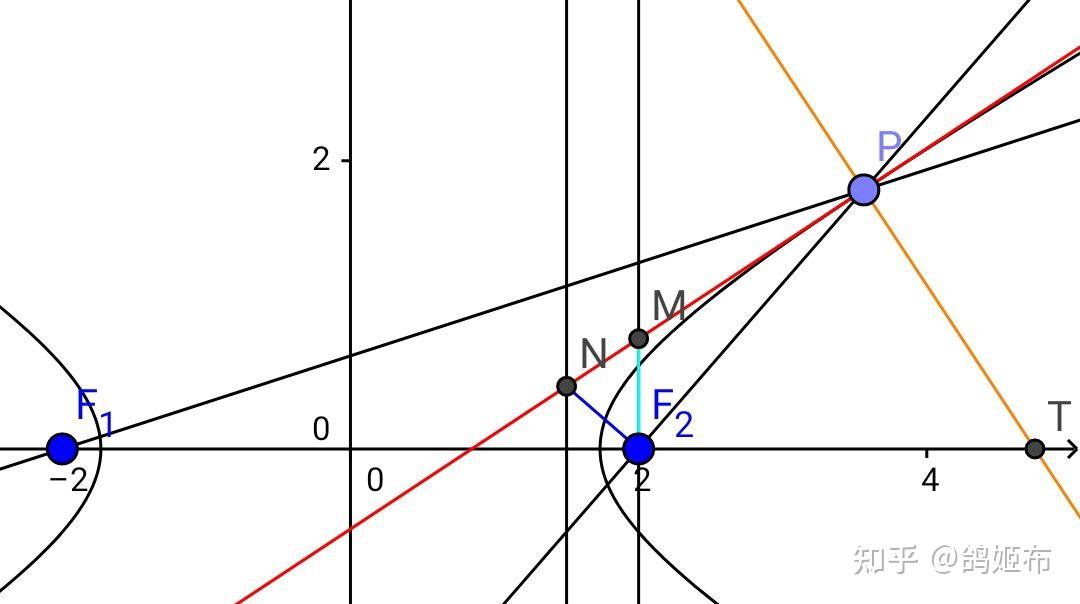光学性质的线其实就是四条，焦点连两条，一个切线一个法线做角平分线。这里注意到 x=\dfrac{3}{2} 是右焦点的极线即右准线，那么 N 是 P,F_2 极线的交点，配极原则知 PF_2 就是 N 的极线，那 NF_2,PF_2 共轭，结合焦点性质就知道 NF_2\bot PF_2 ，这样就有了 \Delta NF_2M\sim\Delta PF_2T ，由角平分线长定理就得到定值

设 P\left( m,n \right) ，则 l：\dfrac{mx}{3}-ny=1 过 P 且 \Delta =0 故其为切线，其交 x=\dfrac{3}{2} 于 N\left( \dfrac{3}{2}，\dfrac{m-2}{2n} \right)

\overrightarrow{FN}·\overrightarrow{FP}=\left( -\dfrac{1}{2}，\dfrac{m-2}{2n} \right)·\left( m-2,n \right)=0 ,所以二线垂直，假设 F_2 关于切线 l 对称点 F 不在 PF_1 上，那么设 F_1F\cap l=P’ ，由三角形的线段长关系， \left| PF_1-PF \right|=\left| PF_1-PF_2 \right|＞\left| PF_1-PF_2 \right|=\left| PF_1-PF \right| ，而 P 在双曲线外，故由双曲线定义矛盾， F’ 在 PF_1 直线上所以切线 l 和法线 l’ 是 PF_1,PF_2 成角的角平分线，设 l\cap x 轴 =T

那么 ∠PNF_2+∠NPF_2=90°=∠NPF_2+∠F_2PT\Rightarrow∠F_2PT=∠PNF_2

同时 ∠NF_2M+∠MF_2P=∠MF_2P+∠PF_2T\Rightarrow∠PF_2T=∠NF_2M

所以 \Delta NF_2M\sim\Delta PF_2T ，角平分线定理 \dfrac{NF_2}{MF_2}=\dfrac{PF_2}{TF_2}=\dfrac{\left| PF_1-PF_2 \right|}{F_1F_2}=\dfrac{\sqrt{3}}{2}

这一题给清楚了代数关系，所以其实代数会更简单，但是如果我们改编一下

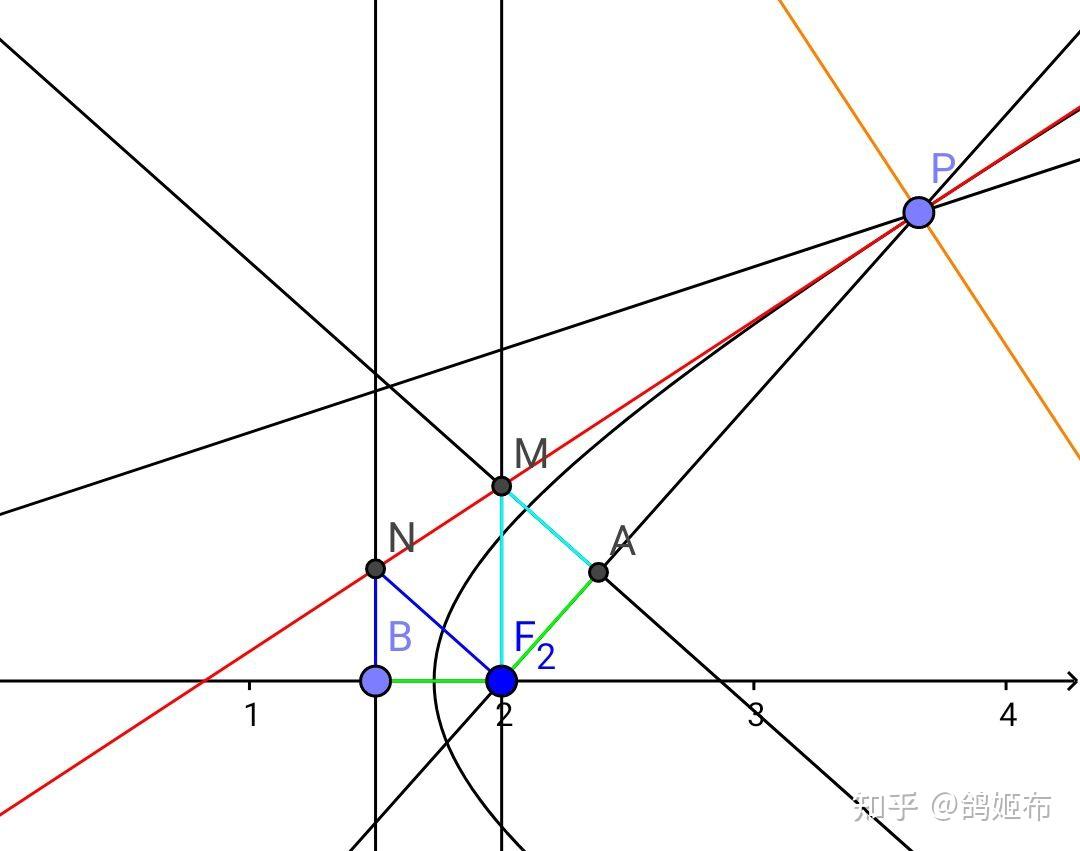
如图，双曲线上任意一点 P 的切线交右焦点 F_2 处的 x 轴垂线于 M ， MA\bot PF_2 , A 在 PF_2 上，求 A 点的轨迹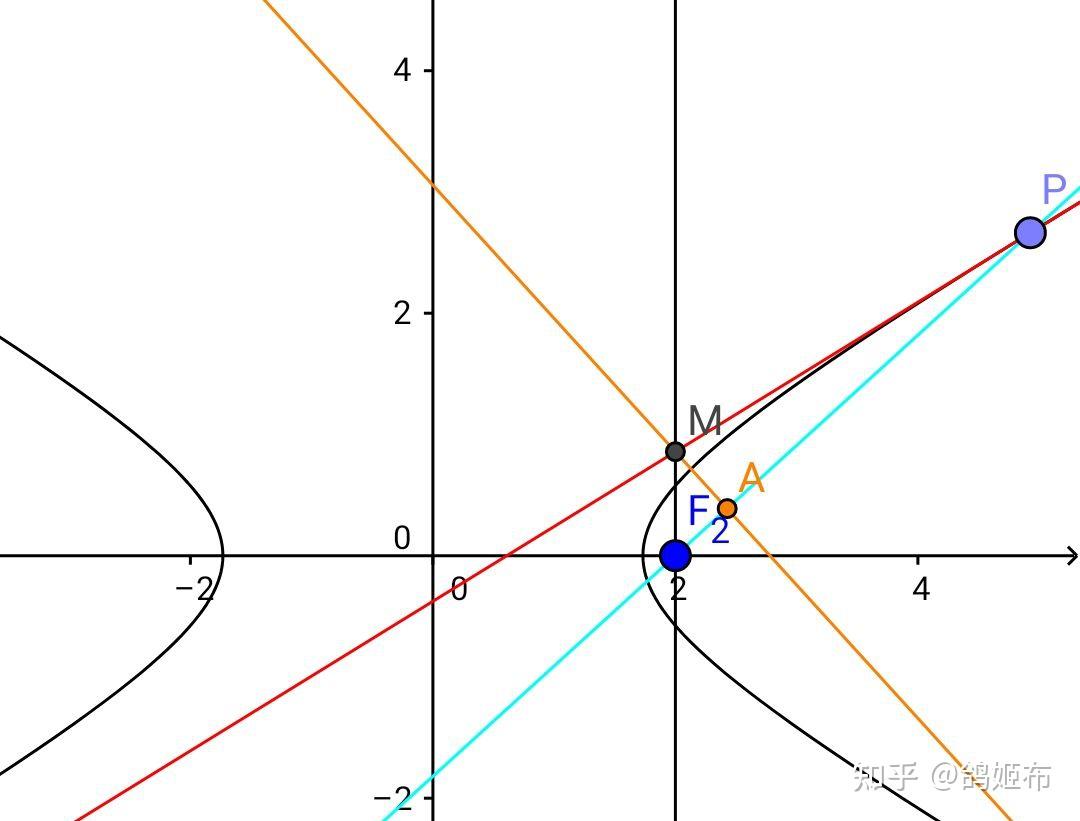

一般涉及全等，相似三角的关系确实会使解析几何的步骤变得复杂

这里只贴出题目辅助线的原理，具体步骤请读者自己思考了

四，尾言

到这里我们对圆锥曲线一些技巧步骤背景的介绍就告一段落，事实上在高考范围内还有一些可能会遇见的小性质，但基本解析上比较难证明的性质以及均在四篇文章里有所涉及，遇到陌生的性质直接按照传统方法进行转化计算代入即可，这里就不对它们一一介绍了。

总而言之，圆锥曲线难在各种背景的综合，比如近年来的透视过定点和几个射影定理，这个时候还是要讲究综合各种方法分析，不拘泥于解析代数，也不拘泥于几何的各种技巧，同时保持一个好的心态。

健康食品 产品推荐 洗护测评 知识科普 牛牛说喷剂 霸王液精华液 七月七胶囊 牛鲨延时喷剂 今枪哥延时喷剂 小牛测评网 赛无双 银豹鹿鞭糖 无限神力虫草鹿血糖