
👉 想了解更多真实延时喷剂测评,可查看: 延时喷剂测评栏目
前言
当光通过材料时,会与材料的原子(离子)和电子相互作用,并产生反射和吸收。通过研究材料的光学性质,可以直接获得有关电子结构、缺陷(或杂质态)以及振动模式等多方面信息。
之一性原理计算光学性质的过程就是计算介电函数的过程,本文将从表征光学性质的7个重要参数的物理意义出发,介绍它们与介电函数的关系,然后给出最简单的密度泛函理论(DFT)加外场扰动的计算方法。最后我们会介绍PWmat计算介电函数的module并着重讨论二维材料的介电函数。
介电函数与光学性质
材料的光学性质都与其介电函数 ε(ω)ε_{(ω)} 有关,本文中的介电函数都是相对介电函数,即其相对于真空的介电函数 ε0ε_{0} 的大小。光是一种电磁波,它在介质中传播时,相当于给介质施加了外场扰动,介质则会对扰动产生响应。考虑最简单的情况,假设入射面在xOy平面内,光的入射方向为z方向,电场分量的偏振方向沿着x,即
介质则会响应外场变化并产生极化
相应的电位移矢量为
显然,介电函数应该是个复数
口语中的介电函数通常指的是 ε(ω)ε_{(ω)} 的实部,它代表相对电容率,即一个材料储存静电能的相对能力的大小,这个值越接近1说明材料的绝缘性越好(越接近真空)。
虚部则代表损耗因子,极化率P 随时间的变化为
在量纲上,P 随时间的导数代表一种电流密度j,这个电流也分为前后两部分,极化电流和传导电流。极化电流和电场相差一个相位π/2,电场在一个周期内做功的平均值为0,因此不消化电磁场的能量;传导电流则具有欧姆定律的电流形式,其电导率为
单位时间内将消耗能量 σE2σE^{2} 。因此,介电函数的虚部代表了介质消耗外场能量的能力。
我们可以通过计算得到材料的介电函数,利用介电函数求得材料的复折射率,并最终得到材料的几个重要的光学参数:
01 复折射率(complex refractive index)
光在介质中传播时的光速为c/n,其中n为折射率,它也应该写成复数的形式
实部即传统定义的折射率,虚部则代表介质内光的衰减(有时也称虚部为“消光系数”),由折射率的定义
因此复折射率和介电函数可以相互表示
或者写成
请注意,为了形式简便,此处我们将常数ε0当作1处理,在实际计算中如果需要就会把这个常数补回来。
02 反射率(reflectivity)
反射光的强度 IrI_{r} 和入射光的强度 I0I_{0} 之比
很显然,它是一个0-1之间的无量纲数,常写成百分数的形式。由于光强 I∝|Ex|2I∝|Ex|^{2} ,在光垂直入射界面的条件下(入射角和折射角均为0)
仔细观察可以发现,这个过程中反射系数和入射方向的正负没有关系,即无论你是从真空到介质还是从介质到真空,反射系数都是一样的。值得注意的是,在考虑复折射率的情况下,反射波和入射波的振幅之比也是个复数
存在辐角θ 意味着反射光和入射光之间会存在相位差,尽管这并不影响反射系数的大小,辐角θ 满足
有时会将反射波与入射波的振幅的比值称为反射系数
但是在黄昆先生的《固体物理学》中,反射系数(reflectance coefficient)的定义与我们这里的反射率相同,都是反射光与入射光的强度之比。这其中可能存在一些历史原因,有待进一步考证。
03 吸收系数(absorption coefficient)
光在介质中传播时沿着z方向的波矢
相应的,电场强度可以表示为
因此光在介质中沿着传播方向以e指数的形式衰减,其衰减的系数为4πωk/c(多乘了系数2是因为光强正比于电场振幅的平方)。从光强的角度,经过界面反射后剩余的光在通过固体的过程中可能被吸收,具体表现为光强随着入射深度z 衰减
其中β 就是吸收系数
在自然单位制下
需要特别注意的是,与反射系数不同,吸收系数是一个实际的物理量,它有属于自己的量纲(通常为 cm−1cm^{-1} )。吸收系数,吸光度和吸收率互为不同的物理量!
04 透射率(tran *** issivity)
通过介质后光的强度 ItI_{t} 和入射光的强度I0I_{0} 的比值
它与材料的反射率R,吸收系数β和材料在入射方向的厚度d(此处为z 方向)都有关
有些时候会与透射系数(tran *** ission coefficient)混用,但是更多的时候,透射系数的定义为透射波与入射波的振幅之比
05 吸光度(absorbance)
光线通过介质前的光强 I0I_{0} 与通过介质后的光强 ItI_{t} 的比值的常用对数。听起来有点绕口,这里直接给一个表达式
不难看出它其实就是透射率倒数的常用对数,可以用一个换底公式将其化简
实际上,即使反射率高达90%,后面一项的数值也只是-2,通常我们也不会讨论一个拥有90%以上的反射率的物质的吸光度。因此,常用的吸光度表达式为
06 吸收率(absorptance/absorptivity)
当光穿过一个材料的过程中,光的强度分为了反射,吸收和透射3个部分,因此材料的吸收率α,反射率R 和透射率τ 满足以下关系
由于界面之间可能存在多重反射,实际的吸收率的形式非常复杂。仅考虑之一次入射-出射过程,则
07 发射率(emissivity)
物体表面热辐射释放的能量与绝对黑体热辐射始放的能量的比值。它也是一个0-1之间的无量纲数,常写成百分数的形式。它与温度T 以及光的频率ω 有关。在特定温度T 下,总的发射率
其中 uBBu_{BB} 为黑体(blackbody, BB)的辐射能量。这本来是个热辐射的概念,但是根据Kirchhoff法则,对于特定频率的光,其吸收率和发射率相等,因此有
对充分厚且不透明的物体,其透射率为0,于是
对黑体,反射率和透射率均为0,于是
对于一般情况,可以直接套用之前吸收率的计算公式。或者按照文献给出的,在上下界面都是平面且经历过多重内部反射时
上述公式的来源可参考:
(1)10.1088/0022-3727/42/15/155412
(2)10.1088/0965-0393/22/7/075004
以上仅仅是最简单的情况,实际的介电函数是一个二阶张量,我们可以通过对称性减少张量的矩阵元的数量,或者直接使用一个正交的晶格使整个张量只有对角元。求解材料的光学性质的关键在于求得复介电函数,但是这个求解过程又触及了密度泛函理论(DFT)的一大痛点,即对外场的响应。DFT的交换关联势中并没有包含动态的介电函数,这意味着第i 个态的电子激发并不会引起其它电子的状态改变。针对上述问题,解决方案有3种:
①直接加一个与时间有关的势能V(r,t ),利用刘维尔方程描述密度算符随时间的变化。这种方法使用的波函数仍然是Kohn-Sham(KS)方程的波函数。该过程的核心在于无规相近似(random phase approximation, RPA)。
②含时密度泛函理论(TDDFT):含时的微扰理论,它可以更好的描述体系对外场的响应函数χ(ω,t )。
③GW近似:直接将动态的介电函数包含在自能项Σ 中。
在这个篇章中,我们将介绍第1种方法,在后续两个篇章中我们将介绍TDDFT方法。GW方法过于昂贵,而且其形式已经高于DFT的框架,在未来将会有专门的篇章介绍GW以及GW+BSE。
DFT+外场扰动
在KS方程的基础上,假设未受扰动时的哈密顿量为 H0H_{0} ,其能量本征值和波函数满足Bloch定理
其中l 代表能带的指标,Ω 为使用的晶胞的体积。此处为没有使用大家熟悉的n 作为能带指标道个歉,因为n 在前后文使用太多次了。其密度算符 ρ0ρ_{0} 满足
其中f 代表Fermi-Dirac分布。
现在我们给该体系施加一个随时间变化的外势 ViV_{i} ,体系会产生一个响应势 VsV_{s} 以屏蔽外场的扰动。此时体系的哈密顿量和密度算符会变为
其中 ρ1ρ_{1} 为受到外场扰动后密度算符的改变。体系的电子气变化满足Liouville方程
由于拥有共同本征态的物理量的对易为0
由Poisson方程可知V 和 ρ1ρ_{1} 存在函数关系,为了简化计算,可以作线性化(linearize)处理,即将二者的乘积视为高阶小量,此时有
又有 ρ0ρ_{0} 不随时间变化。因此
对势V 做Fourier变换,在之一Brillouin zone(BZ)内有
其中的矢量K为倒格矢,对化简后的Liouville方程两端同时求KS本征态的矩阵元有
对于右边的第二项中有
其中的一个因子
求和之后又对r 做积分,这个过程非常繁琐,因此引入RPA:在电子浓度足够大时(固体中很容易满足这个条件),电子的位置在空间的分布是杂乱无规的,在由r 决定的相位因子求和
中,若体系满足平移对称性,则无规则变化(q-q’≠0)的指数项之和为0,即
这也可以理解为电子浓度足够高的情况下,相干叠加的数量级要远大于无规相位的指数相加。刚才的表述是经典动力学中的表述,所以才有“电子浓度”这类表述,源于David在1951年关于相互作用的电子气与等离激元的工作(Phys.Rev.82,625)中。笔者认为这种解释比较直观,所以在此使用。感兴趣的读者可以在李正中先生的《固体理论》的4-4中看到二次量子化表述下的量子运动方程的RPA,即将“异类”之间彼此激发产生的非线性项的求和归零,因此RPA也可以视为一种线性化操作。在微扰理论中,RPA又被称为环形图(ring diagram)近似或圈图修正,在此不继续展开讨论,想继续进阶的读者可以看:
Phys.Rev.106,364(1957)Phys.Rev.111,442(1958)或者找一些多体物理的教材。经过RPA后有
设外势Vi 随着时间的演化为
假设它对体系的影响是绝热的
因此 ρ0ρ_{0} 和 VsV_{s} 都有充足的时间对 ViV_{i} 做出响应,它们对时间的变化形式均与 ViV_{i} 相同
于是Liouville方程的左端可以变成
最终我们得到密度 ρ1ρ_{1} 在KS本征态下的矩阵元
其中
体系对V 的响应表现在极化过程,极化会带来电荷密度的改变(束缚电荷),根据介质中的Maxwell方程组,电荷分为束缚电荷 ρbρ_{b} 和自由电荷 ρfρ_{f}
它们可以分别用与极化矢量P 和和电位移矢量D 的散度来表示
于是,在Gaussian单位制下
从另一个角度理解上述关系,电荷密度的变化完全来源于为了屏蔽外势 V_{i} 而产生的极化。因此,体系响应外场而产生的屏蔽势 V_{s} 和电荷密度的变化可以有一个属于自己的Poisson方程
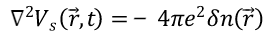
其中电荷密度的变化恰好与 ρ_{1} 在KS本征态下的矩阵元有关
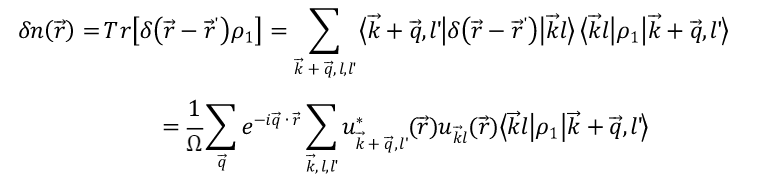
它与V 通过 ρ_{1} 的矩阵元而产生直接的数学关系。于是,我们可以在 V_{s} 和 V 之间建立一种自洽关系
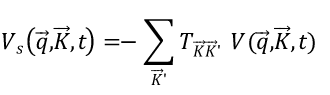
其中
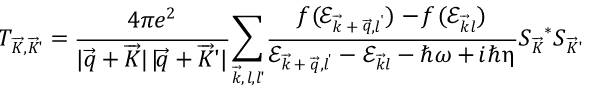
这也是一个矩阵,且矩阵元与倒格矢K,K’ 有关。在单电子近似下,极化率拥有如下形式
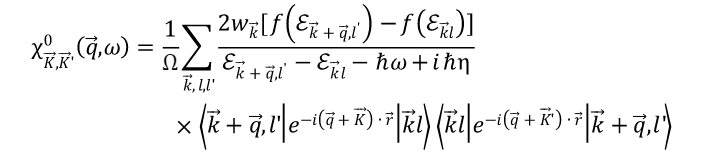
其中 w_{k} 是k点归一化后权重,它们的和为1。于是我们可以看出,矩阵 T_{K,K’} 具有以下意义
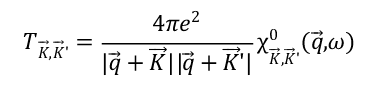
相应的,介电函数的也可以写成与倒格矢K,K’ 有关的矩阵元
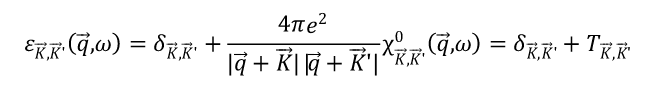
为了求解介电函数的矩阵,仍然需要繁琐的迭代,人们通常只考虑长波极限下的情况。长波极限对应的频率较高,比较符合可见光波段的吸收过程。当|q|远小于|K|时,可以近似的认为标量场f 在一个晶胞范围内的平均值就是标量场在K=0时的值,且f 的平均值的梯度就是f 梯度的平均值,于是
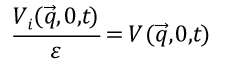
又因为
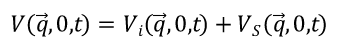
可得
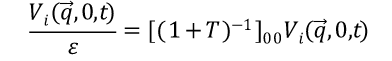
最终我们得到了介电函数的倒数
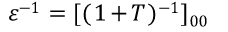
这样得到的介电函数称为“宏观介电函数”
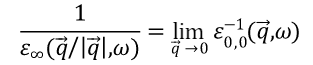
假如介电函数的矩阵没有非对角元,则可以直接求逆
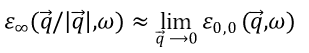
由复数的展开式
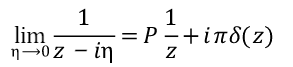
以及二阶张量的表现形式
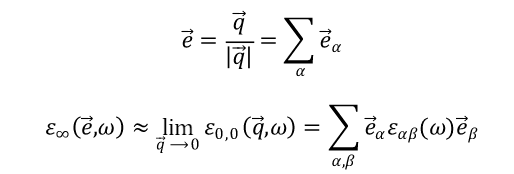
宏观介电函数的虚部可以写作
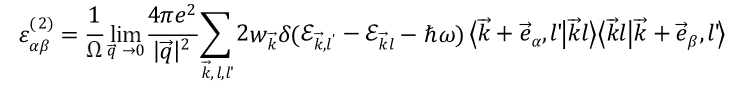
在只有垂直跃迁的情况下,l’ 即为导带CB,l 即为价带VB,再引入原子单位制,则虚部可以改写为
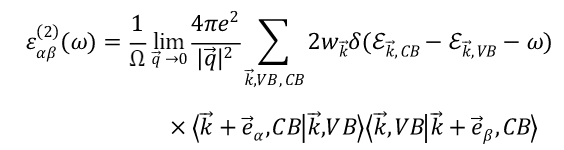
实部则可以直接由虚部通过Kramers-Kronig(KK)变换得到 E_{eff}
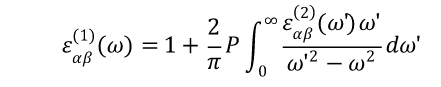
介电函数矩阵经常会存在不为0的非对角元,这是由于微观上单个偶极子处的电场强度并不是平均的宏观电场的强度,而应该是在单个电偶极子中心处的平均电场强度 E_{eff} ,这是一种局域场强。 E_{eff} 和宏观电场的差别来源正是介质中电偶极子的相互作用。在晶体的计算中,这种局域场效应则来源于周期性的势场。有多种方法可以修正局域场效应,我们将在今后的极化性质篇章,结合离子部分的介电函数等因素,详细讨论这个问题。
本部分的推导用到但是不限于以下参考文献:
Phys.Rev.115, 786(1959)
Phys.Rev.129, 62(1963)
Phys.Rev.B.33,7017(1986)PWmat中利用RPA计算光学性质的module
PWmat具有两个module可以利用RPA计算光学性质:module 18的前一部分和module 38。它们的前置工作是类似:
01 做自洽计算,得到波函数
可以选择在这一步就将k-mesh取得很密,同时保证足够的空带数目。也可以选择在这一步使用较少的k-mesh点和空带数,然后在自洽计算的基础上做一个加密K点和空带数目的非自洽计算并输出波函数。
02 利用之一步的波函数做DOS计算
两个module的区别在于对DOS的插值方式不同。计算光学性质需要极密的k-mesh,PWmat提供了两种插值方式,之一种是在每个k点周围以立方体的形式插值,第二种则是在每个k点周围以四面体的形式插值。计算种,推荐使用第二种插值方式。与module 18相比,module 38不仅考虑了局域场效应,还增加了赝势中非局域部分带来的影响。
在实际计算中,可以通过平移算符把对k 的小位移移出Bloch波函数,这样就可以用普通的KS方程的本征态来表示介电函数的虚部
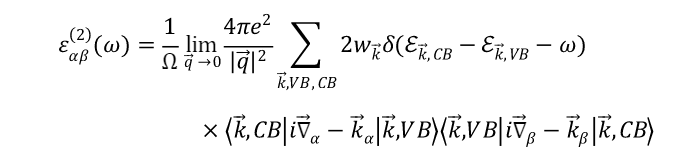
上述展开用了长波极限下的一个近似
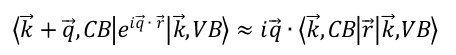
由于有周期性边界条件的存在,在晶体中直接定义位移r 的矩阵元是有问题的。解决方法是将它与晶格的自洽场哈密顿量H_{SCF} 一起考虑
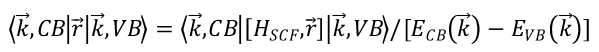
势能中局域的那一部分刚好与位移r 对易,因此哈密顿量只会剩下动能与r 的对易子和非局域势Vnl与r 的对易子
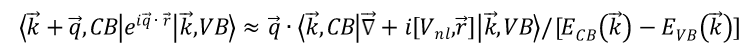
以此修正非局域势对介电函数的影响。
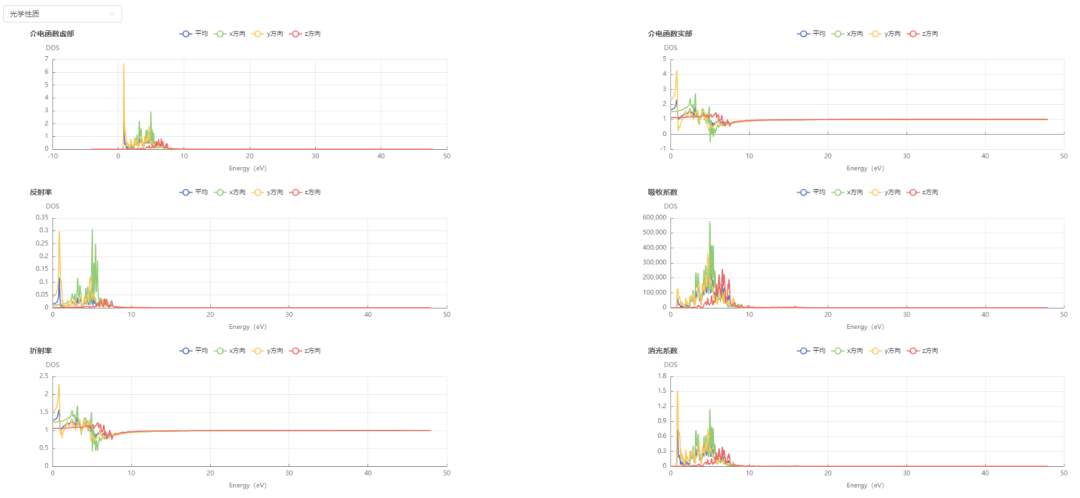
PWmat中有JOB = MOMENT可以进行上述计算,在算完DOS后再计算MOMENT, 然后使用脚本RPA_absorb.x即可获得介电函数。在20220401的版本更新后,这个脚本还会输出复折射率,反射率和消光系数。用户也可以通过脚本RPA_diel_G1G2_000.x来计算宏观静态介电函数。下图展示的是集成module 38的GUI的计算结果(Mcloud 介绍 )。
想要计算发射谱的用户则可以参照module 55。
彩蛋:二维材料的介电函数
在计算二维材料的性质时,为了能使用Bloch波函数,我们会在垂直方向添加真空层,构成一个超胞。于是当我们计算二维材料的介电函数时,实际上是把真空层也当成了bulk的一部分进行计算,这样直接得到的结果肯定是错误的。考虑到二维材料在面内仍然是正常的晶体,由介电函数的虚部和实部的形式
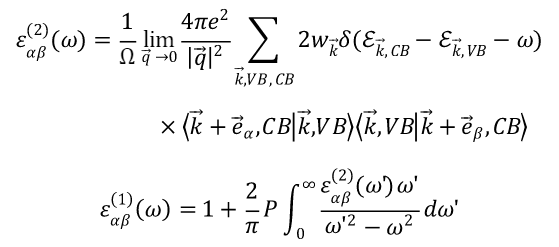
对面内来说,介电函数的错误来自于晶胞的体积取大Ω了,于是面内的函数算出来是偏小的。假设二维材料的厚度为t,真空层方向的晶格常数为c,面内的介电函数与计算所得的介电函数的关系是
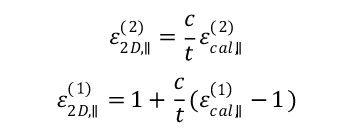
至于如何定义二维材料的厚度,则见仁见智。可以直接用更高和更低的原子z 坐标之差来定义,也可以对z方向的local potential做个积分,去掉能量为真空能级的部分,剩下的部分即为层厚。如果在写paper的时候想偷懒,则做到这一步就可以结束了。你可以说:“假设我的入射光方向是沿着z方向,入射光的偏振方向都在xOy平面内,所以我要计算的所有光学性质只需要面内的分量。”俗称语言的艺术(耍流氓)。
假如遇到一个认真的审稿人,偏要让入射光斜着打;又或者你本身有比较高的学术追求,很想弄清楚垂直层方向的介电函数究竟是什么样的。我们在此提供一个较为简单的思路,参考文献的DOI如下:
10.1039/c8cp04743j
10.1038/s41699-018-0050-x
10.1038/s41467-021-25310-2这种思路的出发点是把垂直层的方向视为两个电容的串联:二维材料和真空。根据串联电容的表达式

于是可以得到
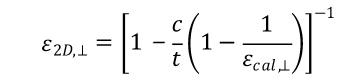
这是宏观静态介电函数的修正方式,它也可以应用于介电函数的实部,而虚部可以近似使用面内的修正方式。
更进一步,我们可以尝试将实部和虚部直接引入电容的关系中,解如下的方程组
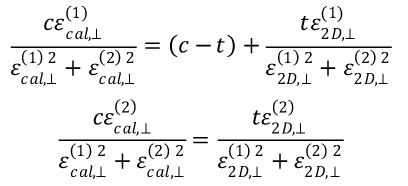
欢迎感兴趣的读者测试并反馈结果。
Mcloud注册登录地址:http://mcloud.lonxun.com/ 推荐码1509
往期专栏文章:北京龙讯旷腾科技有限公司:【龙讯module小课堂】浅谈对gap的认识:PWmat中修正gap的module
更多品牌真实体验、使用方法与风险解析,已整理在:
享久延时喷剂 |
宵战延时喷剂 |
2H2D延时喷剂|
夜劲延时喷剂 |
黑豹延时喷剂 |
宋阳堂延时喷剂
- 上一篇: 圆锥曲线的光学性质及蒙日圆
- 下一篇: 光学性质类毕业论文文献有哪些?

